I. механика

Равноускоренное движение: формулы и примеры

Что такое равноускоренное движение?
Примеры равноускоренного движения
Формула равноускоренного движения
Рекомендуемая литература по теме
Равноускоренное движение, видео

Что такое равноускоренное движение?

Равноускоренным движением в физике считается такое движение, вектор ускорения которого не меняется по модулю и направлению.

Говоря простым языком, равноускоренное движение представляет собой неравномерное движение (то есть идущее с разной скоростью), ускорение которого является постоянным на протяжении определенного промежутка времени.

Представим себе автомобиль, который начинает двигаться, первые 2 секунды его скорость равна 10 м/с, следующие 2 секунды он уже движется со скоростью 20 м/с, а еще через 2 секунды уже со скоростью 30 м/с. То есть каждые 2 секунды он ускоряется на 10 м/с, такое движение и есть равноускоренным.

Отсюда можно вывести предельно простое определение равноускоренного движения: это такое движение любого физического тела, при котором его скорость за равные промежутки времени изменяется одинаково.

Примеры равноускоренного движения

Наглядным примером равноускоренного движения в повседневной жизни может быть велосипед, едущий с горки вниз (но не велосипед, управляемый велосипедистом), или брошенный камень под определенным углом к горизонту.

К слову пример с камнем можно рассмотреть более детально. В любой точке траектории полета на камень действует ускорение свободного падения g. Ускорение g не меняется, то есть остается константой и всегда направлено в одну сторону (по сути, это главное условие равноускоренного движения).

Полет брошенного камня удобно представить в виде сумы движений относительно вертикальной и горизонтальной оси системы координат.

Если вдоль оси Х движение камня будет равномерным и прямолинейным, то вдоль оси Y равноускоренным и прямолинейным.

Формула равноускоренного движения

• Формула скорости при равноускоренном движении будет иметь такой вид:
• V = V0 + at
• Где V0 – это начальная скорость тела, а – ускорение (как мы помним, эта величина является константой), t – общее время полета камня.
• При равноускоренном движении зависимость V(t) будет иметь вид прямой линии.

Ускорение может быть определено по углу наклона графика скорости. На этом рисунке оно равно отношению сторон треугольника АВС.

Чем больше угол β, тем больше наклон и как следствие, крутизна графика по отношению к оси времени, и тем больше будет ускорение тела.

Центростремительное ускорение против центробежного ускорения

Центростремительное ускорение является результатом центростремительной силы, которая действует на объект перпендикулярно и направляет объект к центру, из-за чего движение объекта изменяется и движется по кругу. Чем больше центростремительная сила, тем меньше радиус круга.

Центростремительная сила действует с помощью силы тяжести, трения, натяжения и т. д. Однако, центробежная сила на самом деле называется фиктивными или псевдосилами. Это не сила и используется только в исключительных случаях. Центробежное ускорение есть реактивное ускорение по отношению к центростремительному. ускорение. Можно также сказать, что центробежное ускорение проявляется, когда центростремительное ускорение отсутствует.

Центробежное ускорение противоположно центростремительному ускорению.. Центробежное ускорение имеет центробежную силу, которая направляет объект от центра. Чем больше скорость вращающегося объекта, тем дальше он будет удаляться от центра.

Сам объект применяет центробежную силу. Тенденция объекта всегда состоит в том, чтобы двигаться по прямой линии, но центростремительная сила не позволяет объекту двигаться по прямой линии, и, таким образом, центробежная сила пытается оттянуть объект от центра, чтобы он двигался по прямой линии. . (Не следует путать центробежную силу или ускорение с линейной силой или ускорением).

Подробнее о Примеры центростремительной силы, важные часто задаваемые вопросы.

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч и у вас нет никаких препятствий на пути, то вы скорее всего будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

• Время — в международной системе единиц СИ измеряется в секундах .
• Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка .

Векторные величины (определяются значением и направлением)

• Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
• Перемещение — вектор, проведенный из начальной точки пути в конечную .

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

Скорость может определяться по перемещению и пути, только это будут две разные характеристики. Скорость — это векторная физическая величина, характеризующая быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость — скорость [м/с] — перемещение — время

Средняя путевая скорость V ср.путевая = S/t V ср.путевая — средняя путевая скорость [м/с] S — путь t — время

В чем разница между перемещением и путем? Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости

V ср.путевая = S/t

Подставим значения:

V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уравнение движения

Одна из основных задач механики — определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения x(t) = x + vxt x(t) — искомая координата в момент времени t x — начальная координата vx — скорость тела в данный момент времени [м/с] t — момент времени

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

Уравнение движения при движении против оси x(t) = x − vxt x(t) — искомая координата в момент времени t x — начальная координата vx — скорость тела в данный момент времени [м/с] t — момент времени

Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Получить

Центростремительное ускорение против линейного ускорения

В этом сегменте центростремительное ускорение против ускорения, мы попытаемся расширить наши знания о сходствах и различиях между центростремительным ускорением и линейным ускорением.

Скорость изменения скорости известна как ускорение, но при линейном ускорении объект не изменит своего направления. Он будет двигаться по прямой. Итак, существенным отличием является само направление движения объекта.

При линейном ускорении скорость объекта может увеличиваться или уменьшаться. При центростремительном ускорении меняется только направление скорости. Известно, что объекты, движущиеся прямолинейно, имеют прямолинейное движение.

Есть три основные формулы для нахождения скорости, в которых участвует ускорение. С помощью самих этих формул можно найти ускорение.

v = u + при

х = ut + (1/2) при2

v2 — ты2 = 2 оси

Где,	v = конечная скорость объекта.
	u = Начальная скорость объекта.
	a = ускорение объекта.
	t = время, затраченное объектом.
	x = Расстояние, пройденное объектом.

Линейное ускорение –

Единицей СИ для линейного ускорения является РС2.

Существенное сходство между линейным ускорением и центростремительным ускорением заключается в том, что оба являются векторными величинами, состоящими как из направления, так и из величины. Кроме того, ускорение в любом случае может быть положительным или отрицательным в зависимости от того, увеличивается оно или уменьшается.

Формула центростремительного ускорения

Прежде всего стоит заметить, что движение тела по окружности является сложным. Камень участвует в двух видах движения одновременно: под действием силы он движется к центру вращения, и одновременно по касательной к окружности, от этого центра удаляется. Согласно Второму закону Ньютона, сила, удерживающая камень на веревке, направлена к центру вращения вдоль этой веревки. Туда же будет направлен вектор ускорения.

Пусть за некоторое время t наш камень, равномерно двигаясь со скоростью V, попадает из точки A в точку B. Предположим, что в момент времени, когда тело пересекало точку B, на него перестала действовать центростремительная сила. Тогда за промежуток времени оно попало бы в точку K. Она лежит на касательной. Если бы в тот же момент времени на тело действовали бы только центростремительные силы, то за время t, двигаясь с одинаковым ускорением, оно оказалось бы в точке O, которая расположена на прямой, представляющей собой диаметр окружности. Оба отрезка являются векторами и подчиняются правилу векторного сложения. В результате суммирования этих двух движений за отрезок времени t получаем результирующую движения по дуге AB.

Если промежуток времени t взять пренебрежимо малым, то дуга AB будет мало отличаться от хорды AB. Таким образом, можно заменить движение по дуге движением по хорде. В этом случае перемещение камня по хорде будет подчиняться законам прямолинейного движения, то есть пройденное расстояние AB будет равно произведению скорости камня на время его движения. AB = V х t.

Обозначим искомое центростремительное ускорение буквой a. Тогда пройденный только под действием центростремительного ускорения путь можно рассчитать по формуле равноускоренного движения:

AO = at2 / 2.

Расстояние AB равно произведению скорости и времени, то есть AB = V х t,

AO – вычислено ранее по формуле равноускоренного движения для перемещения по прямой: AO = at2 / 2.

Подставляя эти данные в формулу и преобразуя их, получаем простую и изящную формулу центростремительного ускорения:

a = v2 / R

Словами это можно выразить так: центростремительное ускорение тела, двигающегося по окружности, равно частному от деления линейной скорости в квадрате на радиус окружности, по которой вращается тело. Центростремительная сила в таком случае будет выглядеть так, как на картинке ниже.

Ускорение и скорость

В физике это две разные величины, которые связаны между собой кинематическими уравнениями движения. Обе величины являются векторными, однако в общем случае они направлены по-разному. Ускорение всегда направлено вдоль направления действующей силы. Скорость же направлена вдоль траектории движения тела. Вектора ускорения и скорости будут совпадать друг с другом только тогда, когда внешняя сила по направлению действия совпадает с перемещением тела.

В отличие от скорости, ускорение может быть отрицательной величиной. Последний факт означает, что оно направлено против движения тела и стремится уменьшить его скорость, то есть происходит процесс торможения.

Общая формула, которая связывает модули скорости и ускорения, выглядит так:

v = v + a * t

Это одно из основных уравнений прямолинейного равноускоренного перемещения тел. Оно показывает, что с течением времени скорость возрастает линейно. Если движение будет равнозамедленным, то перед слагаемым a * t следует поставить минус. Величина v здесь является некоторой начальной скоростью.

При равноускоренном (равнозамедленном) движении справедлива также формула:

a¯ = Δv¯ / Δt

От аналогичного выражения в дифференциальной форме оно отличается тем, что здесь ускорение рассчитывается за конечный промежуток времени Δt. Это ускорение называют средним за отмеченный временной промежуток.

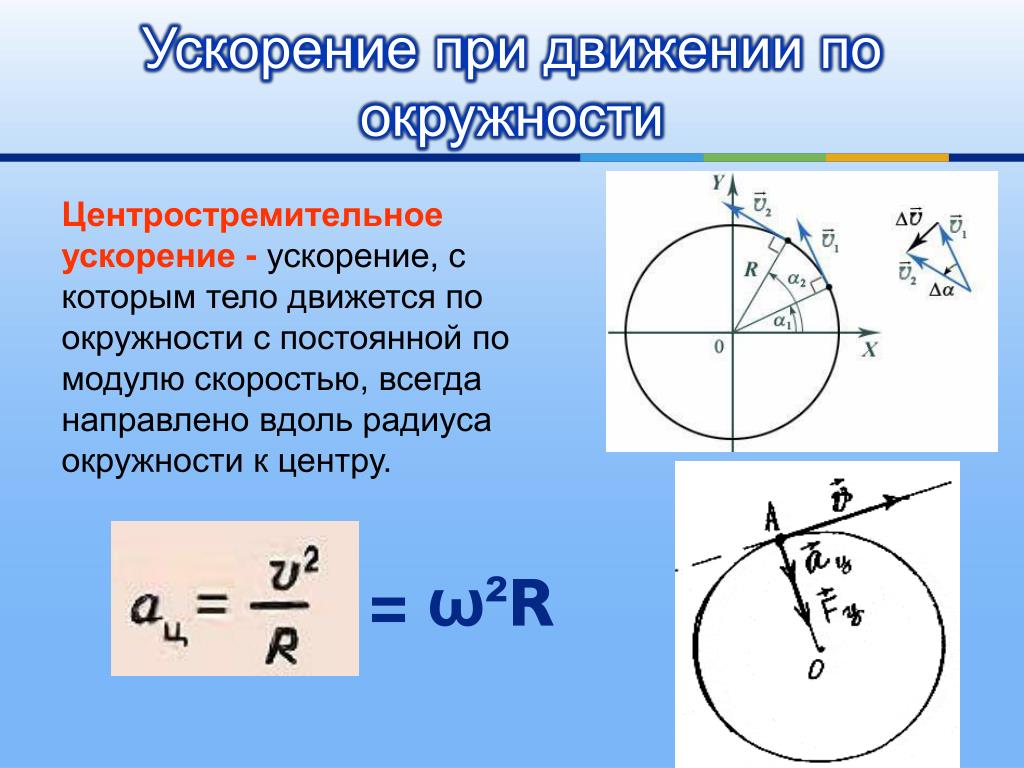
1.6. Движение по окружности window.top.document.title = «1.6. Движение по окружности»;

Движение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах (рис. 1.6.1). Длина дуги связана с углом поворота соотношением

При малых углах поворота Δl ≈ Δs.

Рисунок 1.6.1.Линейное и угловое перемещения при движении тела по окружности

Угловой скоростью ω тела в данной точке круговой траектории называют предел (при Δt → 0) отношения малого углового перемещения Δφ к малому промежутку времени Δt:

Угловая скорость измеряется в рад/с.

Связь между модулем линейной скорости υ и угловой скоростью ω:

При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора

Равномерное движение тела по окружности является движением с ускорением. Ускорение

центростремительным ускорениемυω

Для доказательства этого выражения рассмотрим изменение вектора скорости за малый промежуток времени Δt. По определению ускорения

Векторы скоростей и в точках A и B направлены по касательным к окружности в этих точках. Модули скоростей одинаковы υ_A = υ_B = υ.

Из подобия треугольников OAB и BCD (рис. 1.6.2) следует:

Рисунок 1.6.2.Центростремительное ускорение тела при равномерном движении по окружности

При малых значениях угла Δφ = ωΔt расстояние |AB| =Δs ≈ υΔt. Так как |OA| = R и |CD| = Δυ, из подобия треугольников на рис. 1.6.2 получаем:

При малых углах Δφ направление вектора приближается к направлению на центр окружности. Следовательно, переходя к пределу при Δt → 0, получим:

При изменении положения тела на окружности изменяется направление на центр окружности. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным.

В векторной форме центростремительное ускорение может быть записано в виде

Модель. Равномерное движение по окружности

Если тело движется по окружности неравномерно, то появляется также касательная (или тангенциальная) составляющая ускорения (см. §1.1):

В этой формуле Δυ_τ = υ₂ – υ₁ – изменение модуля скорости за промежуток времени Δt.

Направление вектора полного ускорения определяется в каждой точке круговой траектории величинами нормального и касательного ускорений (рис. 1.6.3).

Рисунок 1.6.3.Составляющие ускорения и при неравномерном движении тела по окружности

Движение тела по окружности можно описывать с помощью двух координат x и y (плоское движение). Скорость тела в каждый момент можно разложить на две составляющие υ_x и υ_y (рис. 1.6.4).

При равномерном вращении тела величины x, y, υ_x, υ_y будут периодически изменяться во времени по гармоническому закону с периодом

Рисунок 1.6.4.Разложение вектора скорости по координатным осям

Изучение законов равноускоренного движения

Изучение законов равноускоренного движения

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ. Поступательное движение тела – это такое движение, при кото¬ром любая прямая, жестко связанная с движущимся телом, остается параллель¬ной самой себе. Положение тела (материальной точки) в декартовой системе координат характеризуется радиусом вектором или тремя его проекциями (X, Y, Z) на оси координат (рис. 1). При движении тела его положение изменяется с течением времени. Рис. 1. Зависимость радиуса, вектора или его проекций от времени называется кинематическим уравнением движения. или X=X(t); Y=Y(t); Z=Z(t) Величина, характеризующая изменение радиус-вектора (иначе говорят вектора перемещения) за единицу времени называется вектором скорости. Вектор средней скорости определяется выражением: , или ; ; . Вектор мгновенной скорости (или скорости в данный момент времени) определяется выражением: ; или ; ; , где Vx,, Vy., Vz — проекции вектора скорости на оси координат. Вектор средней скорости по направлению совпадает с вектором перемещения, а вектор мгновенной скорости направлен по касательной к траектории движения. При движении тела его скорость может изменяться как по модулю, так и по направлению. Величина, характеризующая изменение вектора скорости за единицу времени, называется вектором ускорения. Вектор среднего ускорения определяется выражением: или ; ; . Вектор мгновенного ускорения определяется выражением: или ; ; .

Так как при криволинейном движении скорость может изменяться и по модулю и по направлению, то вектор полного ускорения имеет две составляющие: нормальное ускорение (его ещё называют центростремительным) и касательное ускорение (его ещё называют тангенциальным) (рис. 2):

(1) Нормальное ускорение характеризует быстроту изменения скорости по направлению. Оно направлено по нормали к касательной в данной точки траектории. Модуль этого ускорения определяется выражением , (2) где V – мгновенная скорость; R– радиус кривизны траектории движения в данной точке. Касательное ускорение характеризует быстроту движения скорости по модулю.

Оно направленно по касательной к траектории движения в данной точке. Модуль этого ускорения определяется выражением .

(3) При классификации механических движений тел одновременно по двум признакам – по характеру изменения скорости и по форме траектории – различают четыре вида движения: 1) равномерное прямолинейное: (траектория – прямая линия); 2) неравномерное прямолинейное: (траектория – прямая линия); 3) равномерное прямолинейное: (траектория – кривая линия); 4) неравномерное прямолинейное: (траектория – кривая линия). Частным случаем неравномерного прямолинейного движения является ускоренное движение – движение тела с постоянным ускорением. Законы этого движения могут быть получены из второго закона Ньютона.

Пусть материальная точка массой m движется вдоль оси S c постоянным ускорением а (равноускоренно). Так как ускорение постоянно, то и действующая на точку сила – постоянная.

1) Средняя и мгновенная скорости. 2) Среднее и мгновенное ускорение. 3) Нормальное и касательное ускорение. 4) Законы Ньютона. 5) Равноускоренное движение. Вывод законов движения и скорости.

6) Устройство установки и методика измерения.

Равноускоренное движение

Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.

Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.

В произвольно взятой точке скорость перемещения равна ускорению свободного падения.

Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:

• V0 — начальная скорость;
• A — ускорение (имеет постоянное значение);
• t — время движения.

Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.

Если на оси времени выделить промежуток Δt, то можно предположить, что движение будет равномерным и описываться некоторым параметром, равным мгновенному значению в середине отрезка. Эта моментальная величина является векторной. Она численно равна пределу, который пытается достигнуть скорость за промежуток времени, стремящийся к нулю. В физике это состояние описывается формулой мгновенной скорости: V = lim (Δ s/ Δ t) = r-1(t). То есть, с математической точки зрения, это первая производная.

Исходя из этого можно утверждать, что движение Δs = v*Δt. Так как произведение ускорения на время определяется разницей V -V0, то верной будет запись: S = V0*t + A*t2/2 = (V2 — V20) /2*A.

Из этой формулы можно вывести выражение для нахождения конечной скорости материальной точки: V = (V20 — 2* A * s)½. Если же в начальный момент V0 = 0, то формулу можно упростить до вида: V = (2* A * s)½.

Связь между угловым и тангенциальным ускорением

«Физика — 10 класс»

Угловая скорость.

Каждая точка тела, вращающегося вокруг неподвижной оси, проходящей через точку О, движется по окружности, и различные точки проходят за время Δt разные пути. Так, АА₁ > ВВ₁ (рис. 1.62), поэтому модуль скорости точки А больше, чем модуль скорости точки В. Но радиус-векторы, определяющие положение точек А и В, поворачиваются за время Δt на один и тот же угол Δφ.

Угол φ — угол между осью ОХ и радиус-вектором

Пусть тело вращается равномерно, т. е. за любые равные промежутки времени радиус-векторы поворачиваются на одинаковые углы.

Чем больше угол поворота радиус-вектора, определяющего положение какой-то точки твёрдого тела, за определённый промежуток времени, тем быстрее вращается тело и тем больше его угловая скорость.

Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела υφ к промежутку времени υt, за который этот поворот произошёл.

Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению

Угловая скорость в СИ выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси 0,0000727 рад/с, а точильного диска — около 140 рад/с.

Угловую скорость можно связать с частотой вращения.

Частота вращения — число полных оборотов за единицу времени (в СИ за 1 с).

Если тело совершает ν (греческая буква «ню») оборотов за 1 с, то время одного оборота равно 1/ν секунд.

Время, за которое тело совершает один полный оборот, называют периодом вращения и обозначают буквой Т.

Таким образом, связь между частотой и периодом вращения можно представить в виде

Полному обороту тела соответствует угол Δφ = 2π. Поэтому согласно формуле (1.26)

Если при равномерном вращении угловая скорость известна и в начальный момент времени t = 0 угол φ = 0, то угол поворота радиус-вектора за время t согласно уравнению (1.26)

Если φ ≠ 0, то φ — φ = ωt, или φ = φ ± ωt.

Радиан равен центральному углу, опирающемуся на дугу, длина которой равна радиусу окружности, 1 рад = 57°17’48». В радианной мере угол равен отношению длины дуги окружности к её радиусу: φ = l/R.

Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твёрдого тела, и осью ОХ увеличивается (рис. 1.63, а), и отрицательные, когда он уменьшается (рис. 1.63, б).

Тем самым мы можем найти положение точек вращающегося тела в любой момент времени.

Связь между линейной и угловой скоростями.

Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть её отличие от угловой скорости.

Мы уже отмечали, что при вращении абсолютно твёрдого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова.

Установим связь между линейной скоростью любой точки вращающегося тела и его угловой скоростью. Точка, лежащая на окружности радиусом R, за один оборот пройдёт путь 2πR. Поскольку время одного оборота тела есть период Т, то модуль линейной скорости точки можно найти так:

Так как ω = 2πν, то

Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше её линейная скорость. Для точек земного экватора υ = 463 м/с, а для точек на широте Санкт-Петербурга υ = 233 м/с. На полюсах Земли υ = 0.

Модуль центростремительного ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:

Запишем все возможные расчётные формулы для центростремительного ускорения:

Мы рассмотрели два простейших движения абсолютно твёрдого тела — поступательное и вращательное. Однако любое сложное движение абсолютно твёрдого тела можно представить как сумму двух независимых движений: поступательного и вращательного.

На основании закона независимости движений можно описать сложное движение абсолютно твёрдого тела.

Кинематика — Физика, учебник для 10 класса — Класс!ная физика

Угловой путь

Для начала, вспомним, что линейное перемещение – это разница между конечным и начальным положением точки на оси (рис. 1).

\

Рис. 1. Линейное перемещение равно разности между конечным и начальным положениями точки на оси

Рассмотрим теперь колесо (рис. 2). На горизонтальной линии, проходящей через диаметр колеса, справа отметим красную точку, от которой мы начнем отсчитывать углы. Условимся считать, что возле этой точки находится нулевой угол.

Рис. 2. Точка из положения 1 сместилась в положение 2, пройдя угловой путь

На ободе колеса выберем точку, например — ниппель. Сначала ниппель находился в точке 1. Точка 1 сдвинута на угол \(\gamma_{1}\) относительно начала отсчета.

Будем вращать колесо в направлении, обозначенном синей стрелкой. Повернем колесо на некоторый угол, так, чтобы к концу движения ниппель переместился в точку, обозначенную цифрой 2 на рисунке. Эта точка смещена на угол \(\gamma_{2}\) по отношению к началу отсчета.

По аналогии с поступательным движением, угловой путь, который прошел ниппель — это разница (разность) угловых положений точек 1 и 2.

\

\(\varphi \left( \text{рад}\right)\) – угловой путь измеряется в радианах.

Угловой путь – это угол, на который повернулся ниппель, по отношению к его начальному положению.

Вращение тел

Под вращением понимают тип движения, при котором траектория перемещающегося тела представляет собой окружность. Вращение может происходить вокруг оси или вокруг фиксированной точки. Вращение колеса, планет по своим орбитам, спортсменов во время соревнований по фигурному катанию — все это примеры указанного типа движения.

По аналогии с линейным перемещением, главной формулой динамики вращения является следующая:

Здесь M и I — моменты силы и инерции, соответственно, α — ускорение угловое.

Для описания вращения удобно пользоваться не линейной, а угловой скоростью. Она определяется так:

Где θ — угол, на который тело повернулось за время t. С записанным ускорением α скорость ω связана следующим равенством:

Для измерения всех угловых величин используются радианы.

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

Рассмотри твердое тело, вращающееся вокруг неподвижной оси . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость равна производной угла поворота по времени . При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Угловое ускорение равно производной угловой скорости по времени:. Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Скорость точки при вращательном движении тела вокруг неподвижной оси

Рассмотрим точку , принадлежащую твердому телу. Опустим из нее перпендикуляр на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки является окружность (или дуга) с центром в точке радиуса .

Абсолютное значение скорости точки определяется по формуле:. Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .

Касательное (или тангенциальное) ускорение точки определяется аналогично скорости:. Оно направлено по касательной к окружности, перпендикулярно . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

Ускорение точки при вращательном движении тела вокруг неподвижной оси

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину.

Полное ускорение точки , или просто ускорение, равно векторной сумме касательного и нормального ускорений:. Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки определяется по формуле:.

Поступательное прямолинейное движение

Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось вдоль его линии движения. Пусть есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:. При , вектор скорости направлен вдоль оси . При – противоположно этой оси.

Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:. При , вектор ускорения направлен вдоль оси . При – противоположно.

Соприкосновение тел без проскальзывания

Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка принадлежит первому телу, а точка – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:. Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:. Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:.

Вывод формулы

Математическое обоснование формулы для нахождения центростремительного ускорения при движении по окружности либо другой кривой траектории строится следующим образом. Величина убыстрения вычисляется, когда направление ускорения меняется, а вектор же всегда направлен к центру, причём его модуль равняется квадрату скорости, делённому на радиус: a = V2 / r.

Можно представить спутник, который движется по круговой орбите вокруг Земли. Некоторые космические тела описывают окружность и вращаются против часовой стрелки. Радиус-вектор удобно определить как функцию времени. Он изменяется при вращении тела по окружности P(t). Итак, за начало координат можно взять точку, обозначающую планету Земля и провести через неё координатные оси.

Нужно определить вектор между положительной полуосью P(x) и радиус-вектором Q. Орбита имеет радиус R, величина которого постоянна. Модуль изменяющегося радиус-вектора будет равняться r || p (+)|| = r. Чтобы записать вектор через компоненты, используются основы тригонометрии, позволяющие выполнить разложение по базису.

В какой-то момент времени радиус-вектор будет обладать модулем r. Его угол равняется по иксу компоненте r * cosQ, а по игреку — r * sinQ. Параметр в любой момент может быть выражен через сумму икс и игрек компонентов: p (t) = r * cosQ (t) * I + r * sinQ (t) * j, где I — базис для икса компоненты, направленной вдоль оси ординаты, а j — параллельно оси абсциссы.

Производная от всего этого выражения и будет вектором скорости как функция от времени: V (t) = dp / dt = r (-sinQ (t)) * w * I + r * cosQ (t) * w * j. Сделав преобразования, можно получить выражение следующего вида: V (t) = -w * r (sinQ (t) * I — cos Q (t) * j). Теперь нужно взять производную от скорости, что является ускорением по времени: a (t) = dV / dt = =w * r * (cos (Q (t) * w * I + sin (Q (t) * w * j) = — w2 * r * (cos (Q (t) * I + sinQ (t) * j) = — w2 * p (t).

В итоге получится: ac = w 2 * r = (V/r)2 * r. Следует заметить, что направление центростремительного ускорения будет внутрь. В полученной формуле r сокращается и получается доказываемая формула: ac = V2 / r.