Вес тела и невесомость

Невесомость

Если тело вместе с опорой свободно падает,
то a=g, и из
формулы (12) следует, что
P=0.

Исчезновение веса при движении опоры с ускорением
свободного падения называется
невесомостью.

Состояние невесомости наблюдается в самолете
или космическом корабле при движении
с ускорением свободного падения
независимо от направления и значения
модуля скорости их движения. Действительно,
если представить себе ситуацию, когда наш
лифт с кубиком помимо движения с ускорением
свободного падения находится в состоянии
движения с постоянной скоростью в направлении
оси OX, перпендикулярной оси
OY, все наши предыдущие
рассуждения остаются в силе. Таким образом
движение с постоянной скоростью, вектор
которой имеет произвольное направление
относительно вектора ускорения свободного
падения наших тел, не оказывает влияния
на состояние невесомости. За пределами
земной атмосферы при выключении
реактивных двигателей (становится равной
нулю сила тяги двигателей) на космический
корабль действует только сила всемирного
тяготения. Под действием этой силы
космический корабль и все тела, находящиеся
в нем, движутся с одинаковым
ускорением;
поэтому на корабле начинает наблюдаться явление
невесомости.

Что измеряют весы?

Многие скажут – «смотря какой конструкции это будут весы».

Обратимся к словарям.

Толковые словари С.И.Ожегова (с. 62) и Д.Н.Ушакова (т. 1, с. 262) утверждают, что весы – это прибор для измерения веса. При этом на с. 64 в первом словаре и т. 1, с. 273 во втором глагол «взвесить» означает – определить вес.

Энциклопедический словарь (1953), т. 1, с. 296, Физический энциклопедический словарь (1960), т. 1, с. 220, Малая Советская Энциклопедия (1958), т. 2, с. 343 (все под редакцией Б.А.Введенского) и Большая Советская Энциклопедия, под редакцией А.М.Прохорова (1971), т. 4, с. 568 указывают, что весы – это прибор для определения массы тела.

Все издания утверждают, что пружинные весы измеряют вес. В то же время многие издания утверждают, что рычажные (равноплечие) весы измеряют массу. Только в учебнике Б.М.Яворского, А.А.Пинского «Основы физики», т. 1, и Г.С.Ландсберга «Элементарный учебник физики», т. 1, указывается, что рычажные весы измеряют вес. Чему должен верить читатель?

Действительно, с пружинными весами все ясно. В их «весовой» функции даже невозможно усомниться.

А на рычажных весах вроде бы очень удобно измерять массу тела. Ведь при балансе чашек (в случае равенства весов тел) мы тут же можем судить о равенстве масс исследуемого тела и уравновешенных гирь.

Кроме того, рычажные весы имеют еще одно неоспоримое удобство. Равновесие чашек с грузами не нарушается, если их перевести на полюс, экватор, с Земли на Луну и т.д. (вес тела при этом меняется, а масса нет!).

Думается, равновесие рычажных весов здесь не нарушается не столько из-за постоянства масс тел, сколько из-за одинаковой кратности изменения весов тел на обеих чашках.

И почему ни одни весы ничего не показывают в состоянии полной невесомости (ведь масса тела остается неизменной и сила тяжести также!)?

Да потому, что в состоянии полной невесомости вес тела равен нулю, вот весы и фиксируют нулевой вес!

А как быть тогда, когда мы на рычажных весах взвешиваем пуховое тело или хлопок (вату)? Ведь это объемное тело, испытывающее ощутимое действие выталкивающей силы воздуха, которая в большинстве случаев незначительная и на гири, стоящие на второй чашке весов, почти не действует. При балансе чашек можно еще говорить о равенстве весов тел на чашках, но именно масса пухового тела при балансе чашек будет обязательно большей, чем совокупная масса гирь. И здесь уже рычажные весы не могут дать точный ответ о массе пухового тела!

А если в состоянии полной невесомости пытаться определить массу тела, то неизбежно нужно будет создать какое-то силовое взаимодействие этого тела с другим телом. Иначе говоря, весы все-таки в принципе созданы для определения силы, и «лишить» их своей весовой функции практически невозможно. Поэтому останавливаемся на точке зрения, что весы любой конструкции измеряют вес, но иногда позволяют оценить и массу. Разговоры о том, что весы градуируются в граммах, килограммах, тоннах и каратах, сути весовой функции весов не меняют.

В интересах доказательства назначения весов для определения массы предлагают даже ввести термин «массометр» («Толковый словарь школьника по физике», 1999, авторы К.К.Гомоюнов, М.Ф.Кесаманлы, Т.Г.Кесаманлы, с 39). Думается, что это не получится. Ведь с древних времен человека интересовала масса как мера тяжести (т.е. проблема веса) гораздо в большей степени, чем масса инертная.

И ссылки на то, что в седьмом классе мы учим детей определять массу на весах, ничего не меняют. Мы видим, какое сложное понятие – «вес тела», и не усложняем жизнь маленьким учащимся. А научить их практически пользоваться весами нужно еще с малых лет.

Задачи на вес и невесомость с решениями

Задача №1. Задача на расчет веса тела, движущегося с ускорением

Условие

Груз массой 20 кг лежит на полу лифта, который движется вверх с ускорением а=4 м/с^2. Найти вес тела.

Решение

По второму закону Ньютона (в векторной форме и в проекции на ось y):

По третьему закону Ньютона:

Ответ: 280 Ньютонов

Задача №2. Задача на вычисление веса тела в жидкости

Условие

Шар радиусом 10 сантиметров имеет массу 20 килограмм. Сколько она будет весить в воде?

Решение

Вес шара в воздухе:

На тело, погруженное в жидкость, действует сила Архимеда:

Ответ: P=158 Н.

Условие

Тело весит 400 Ньютонов. Какова его масса?

Решение

Ответ: 60 кг.

Задача №4. Вычисление веса жидкости

Условие

Какой вес имеет вода, полностью заполнившая литровую бутылку?

Решение

Зная объем воды и взяв из справочника ее плотность, вычислим массу воды:

Ответ: Р=10 Н.

Задача №5. Нахождение веса при свободном падении. Невесомость на Земле

Условие

Лифт с человеком срывается в шахте и свободно падает вниз, пока не сработает система безопасности. Чему в момент падения равен вес человека.

Решение

Лифт и человек движутся с ускорением a=g. Согласно второму и третьему законам Ньютона, вес человека в этом случае будет вычисляться по формуле:

Другими словами, человек никак не действует на опору, так она падает одновременно с ним. Типичный пример, когда вес равен нулю.

Ответ: P=0 Н.

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Доклад 2

Невесомость – это физическое состояние, при котором отсутствует какое-либо давление на тело, а из сил остаётся только сила тяжести.

Одна из характерных черт состояния невесомости – отсутствие веса тела. Она также происходит от отсутствия давления. В быту весом принято называть массу тела, и из-за ошибок в использовании терминов некоторые считают что тело в невесомости ничего не весит, не имеет массы. Это не так. Масса – это скалярная величина, которая меняется только при изменении физической конфигурации тела. В то время как вес – это сила, характеризующая то, как тело давит на опору под действием силы тяжести. А так как в невесомости нет давления, то нет и веса и ответной пропорциональной реакции опоры (или подвеса), которые совместно образуют на Земле то, что человек ощущает как “весомость”.

Один из способов достижения невесомости – скомпенсировать силу гравитации другой силой. Часто такой силой является сила инерции, возникающая при ускоренном движении тела. Рассмотрим несколько случаев, в которых возникает невесомость.

Первый такой случай – падающая (или просто движущаяся с определенным ускорением) кабина лифта. В стоящей на месте кабине пассажир давит на опору – пол – с силой, равной его весу. Сила ответной реакция пола примерно равна ей. Но когда кабина начинает двигаться с ускорением по направлению, параллельному вектору приложения силы тяжести (то есть вниз), возникает сила инерции, создающая в пространстве внутри кабины эффект невесомости, распространяющийся и на пассажира. Впрочем, говорить о невесомости как о самостоятельном явлении несколько неправильно: она может существовать только при наличии человека или любого другого объекта, у которого есть вес и который может оказывать воздействие на опору или подвес. Нечто похожее происходит и в кабине самолета, резко меняющего направление, однако в обоих случаях невесомость может возникнуть лишь на несколько секунд.

Самый очевидный пример невесомости – космос, к примеру пространство внутри космической станции. Здесь ее также обеспечивает сила инерции, однако причина ее возникновения не так очевидна. Станция совершает постоянное движение по орбите Земли с развитым при выходе на нее ускорением, как бы совершая постоянное “падение”, в результате чего появляется невесомость – неспособность тел оказывать давление на опору.

7, 9 класс

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Имеются две абсолютно упругие пружины. Под действием одной и той же силы первая пружина удлинилась на 8 см, а вторая — на 4 см. Сравните жёсткость \( k_2 \) второй пружины с жёсткостью \( k_1 \) первой пружины.

1) \( k_1=k_2 \)
2) \( 4k_1=k_2 \)
3) \( 2k_1=k_2 \)
4) \( k_1=2k_2 \)

2. Имеются две абсолютно упругие пружины: одна жёсткостью 200 Н/м, другая жёсткостью 400 Н/м. Сравните силу упругости \( F_2 \), возникающую во второй пружине, с силой упругости \( F_1 \), возникающей в первой пружине, при одинаковом их удлинении.

1) \( F_2=F_1 \)
2) \( F_2=4F_1 \)
3) \( 2F_2=F_1 \)
4) \( 0.5F_2=F_1 \)

3. Ученик, растягивая пружину динамометра последовательно на 1Н, 2Н, ЗН и 4Н, каждый раз измерял её удлинение и результаты измерений вносил в таблицу. Определите по данным таблицы жёсткость пружины динамометра.

1) 0,02 Н/м
2) 0,5 Н/м
3) 2 Н/м
4) 50 Н/м

4. На рисунке приведены графики зависимости силы упругости от удлинения. Сравните жёсткость пружин.

1) \( k_2=k_1 \)
2) \( k_2>k_1 \)
3) \( k_2<k_1 \)
4) \( k_2\geq k_1 \)

5. Учащийся выполнял эксперимент по измерению удлинения \( x \) пружин при подвешивании к ним грузов. Полученные учащимся результаты представлены на рисунке в виде диаграммы. Какой вывод о жёсткости пружин \( k_1 \) и \( k_2 \) можно сделать из анализа диаграммы, если к концам пружин были подвешены грузы одинаковой массы?

1) \( k_2=4k_1 \)
2) \( k_1=2k_2 \)
3) \( k_2=2k_1 \)
4) \( k_1=k_2 \)

6. Под действием силы 3 Н пружина удлинилась на 4 см. Чему равна сила, под действием которой удлинение этой пружины составит 6 см?

1) 3,5 Н
2) 4 Н
3) 4,5 Н
4) 5 Н

7. Две пружины растягиваются одинаковыми силами. Жёсткость первой пружины \( k_1 \) в 2 раза больше жесткости второй пружины \( k_2 \). Удлинение первой пружины \( \Delta l_1 \), удлинение второй пружины \( \Delta l_2 \) равно

1) \( 0.5\Delta l_1 \)
2) \( 0.67\Delta l_1 \)
3) \( 1.5\Delta l_1 \)
4) \( 2.5\Delta l_1 \)

8. В лифте, движущемся вниз равноускоренно из состояния покоя, стоит ящик. Модуль веса ящика

1) равен модулю силы тяжести
2) больше модуля силы тяжести
3) меньше модуля силы тяжести
4) увеличивается с увеличением скорости лифта

9. Человек испытывает перегрузки при

1) равномерном движении вниз
2) равномерном движении вверх
3) равноускоренном движении вверх из состояния покоя
4) равноускоренном движении вниз с ускорением свободного падения

10. Различие веса тела на экваторе и на полюсе можно обнаружить

А. Взвешивая тело на рычажных весах
Б. Взвешивая тело на пружинных весах

Правильный ответ

1)только А
2)только Б
3) и А, и Б
4) ни А, ни Б

11. Установите соответствие между физической величиной (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Модуль силы упругости пружины
Б. Жёсткость пружины
B. Модуль удлинения пружины

ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) уменьшается
2) увеличивается
3) не изменяется

12. Из приведённых ниже высказываний выберите два верных и запишите их номера в таблицу.

1) Закон Гука справедлив при любых деформациях.
2) Сила упругости направлена в сторону, противоположную деформации.
3) Жёсткость зависит только от материала, из которого изготовлено тело.
4) Вес тела всегда равен действующей на него силе тяжести.
5) Вес приложен к опоре или к подвесу.

Вес тела

Весом тела называется сила, с которой данное тело давит на опору или растягивает подвес вследствие притяжения данного тела к Земле.

Установим основные характеристики этой силы – причину ее возникновения, модуль и направление. Рассмотрим тело, подвешенное на пружине (Рис. 1.). Под действием силы тяжести тело стремится двигаться вниз, увлекая за собой нижний конец пружины. В свою очередь, пружина деформируется, что вызывает появление в ней силы упругости.

Рис. 1. Тело, подвешенное на пружине

Под действием силы упругости, которая приложена к верхнему краю тела, это тело, в свою очередь, также деформируется, возникает другая сила упругости, обусловленная деформацией тела. Эта сила приложена к нижнему краю пружины. Кроме того, она равна по модулю силе упругости пружины и направлена вниз. Именно эту силу упругости тела мы и будем называть его весом, то есть вес тела приложен к пружине и направлен вниз.

После того как колебания тела на пружине затухнут, система придет в состояние равновесия, в котором сумма сил, действующих на тело, будет равна нулю. Это значит, что сила тяжести рана по модулю и противоположна по направлению силе упругости пружины (Рис. 2). Последняя равна по модулю и противоположна по направлению весу тела, как мы уже выяснили. Значит, сила тяжести по модулю равна весу тела. Данное соотношение не универсально, но в нашем примере – справедливо.

Рис. 2. Вес и сила тяжести

Приведенная формула не означает, что сила тяжести и вес – одно и то же. Эти две силы разные по своей природе. Вес – это сила упругости, приложенная к подвесу со стороны тела, а сила тяжести – это сила, приложенная к телу со стороны Земли.

Рис. 3. Вес и сила тяжести тела на подвесе и на опоре

Невесомость

Выясним некоторые особенности веса. Вес – это сила, с которой тело давит на опору или растягивает подвес, из этого следует, что если тело не подвешено или не закреплено на опоре, то его вес равен нулю. Данный вывод кажется противоречивым нашему повседневному опыту. Однако он имеет вполне справедливые физические примеры.

Если пружину с подвешенным к ней телом отпустить и позволить ей свободно падать, то указатель динамометра будет показывать нулевое значение (Рис. 4). Причина этого проста: груз и динамометр движутся с одинаковым ускорением (g) и одинаковой нулевой начальной скоростью (V0). Нижний конец пружины движется синхронно с грузом, при этом пружина не деформируется и силы упругости в пружине не возникает. Следовательно, не возникает и встречной силы упругости, которая является весом тела, то есть тело не обладает весом, или является невесомым.

Рис. 4. Свободное падение пружины с подвешенным к ней телом

Состояние невесомости возникает благодаря тому, что в земных условиях сила тяжести сообщает всем телам одинаковое ускорение, так называемое ускорение свободного падения. Для нашего примера мы можем сказать, что груз и динамометр движутся с одинаковым ускорением. Если на тело действует только сила тяжести или только сила всемирного тяготения, то это тело находится в состоянии невесомости

Важно понимать, что в этом случае исчезает только вес тела, но не сила тяжести, действующая на это тело

Состояние невесомости – не экзотика, довольно часто многие из вас его испытывали – любой человек, подпрыгивающий или спрыгивающий с какой либо высоты, до момента приземления находится в состоянии невесомости.

Рассмотрим случай, когда динамометр и прикрепленное к его пружине тело движутся вниз с некоторым ускорением, но не совершают при этом свободного падения. Показания динамометра уменьшатся по сравнению с показаниями при неподвижном грузе и пружине, значит, вес тела стал меньше, чем он был в состоянии покоя. В чем причина такого уменьшения? Дадим математическое объяснение, опираясь на второй закон Ньютона.

Рис. 5. Математическое объяснение веса тела

На тело действуют две силы: сила тяжести, направленная вниз, и сила упругости пружины, направленная вверх. Эти две силы сообщают телу ускорение. и уравнение движения будет иметь вид:

m = + m

Выберем ось y (Рис. 5), поскольку все силы направлены вертикально, нам достаточно одной оси. В результате проецирования и переноса слагаемых получим – модуль силы упругости будет равен:

ma = mg — Fупр

Fупр = mg — ma,

где в левой и правой части уравнения стоят проекции сил, указанных во втором законе Ньютона, на ось y. Согласно определению, вес тела по модулю равен силе упругости пружины, и, подставив ее значение, получим :

P = Fупр = mg — ma = m( g — а)

Вес тела равен произведению массы тела на разность ускорений. Из полученной формулы видно, что если модуль ускорения тела меньше модуля ускорения свободного падения, то вес тела меньше силы тяжести, то есть вес тела, движущегося ускоренно, меньше веса покоящегося тела.

Рассмотрим случай, когда тело с грузиком движется ускоренно вверх (Рис. 6).

Стрелка динамометра покажет значение веса тела большее, чем покоящегося груза.

Рис. 6. Тело с грузиком движется ускоренно вверх

Тело движется вверх, и его ускорение направлено туда же, следовательно, нам необходимо поменять знак проекции ускорения на ось у.

Из формулы видно, что теперь вес тела больше силы тяжести, то есть больше веса покоящегося тела.

Увеличение веса тела, вызванное его ускоренным движением, называется перегрузкой.

Это справедливо не только для тела, подвешенного на пружине, но и для тела, укрепленного на опоре.

Рассмотрим пример, в котором проявляется изменение тела при его ускоренном движении (Рис. 7).

Автомобиль движется по мосту выпуклой траектории, то есть по криволинейной траектории. Будем считать форму моста дугой окружности. Из кинематики мы знаем, что автомобиль движется с центростремительным ускорением, величина которого равна квадрату скорости, деленной на радиус кривизны моста. В момент нахождения его в наивысшей точке, это ускорение будет направлено вертикально вниз. Согласно второму закону Ньютона это ускорение сообщается автомобилю равнодействующей силой тяжести и силой реакции опоры.

m = + m

Выберем координатную ось у, направленную вертикально вверх, и запишем это уравнение в проекции на выбранную ось, подставим значения и проведем преобразования:

Рис. 7. Наивысшая точка нахождения автомобиля

Вес автомобиля, по третьему закону Ньютона, равен по модулю силе реакции опоры (), при этом мы видим, что вес автомобиля по модулю меньше силы тяжести, то есть меньше веса неподвижного автомобиля.

Вес тела

В технике и быту широко используется понятие
веса тела.

Весом тела называют силу,
с которой тело вследствие его притяжения
к Земле действует на горизонтальную опору
или подвес.

Вес тела , то есть сила, с которой
тело действует на опору или подвес, и сила упругости
,
с которой опора действует на тело
(см. рис. 3), в соответствии
с третьим законом
Ньютона равны по модулю и противоположны по
направлению:

(6)

Если тело находится в покое на горизонтальной
поверхности или движется равномерно прямолинейно
и на него действуют только сила тяжести
(она показана
на рисунке зеленым цветом) и сила упругой
реакции (красная стрелка, направленная вверх)

со стороны опоры, то из равенства нулю этих сил
следует равенство:

(7)

Сопоставив выражения (6) и (7), получим:

(8)

В том случае, если сила тяжести окажется
по величине больше силы упругой реакции
опоры, и опора, и тело начинают двигаться
с ускорением, величина которого определяется
разностью этих сил.
При ускоренном движении тела и опоры вес

будет отличаться от силы тяжести
. По второму
закону Ньютона при ускоренном движении
тела (нашего кубика) с ускорением
,
имеющего массу
m, под
действием силы тяжести

и силы упругой реакции
,
выполняется равенство:

(9)

(10)

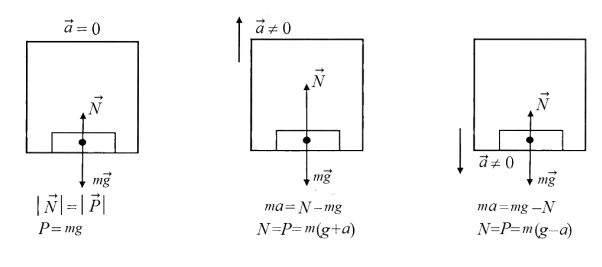
Рассмотрим случай ускоренного движения лифта
(см. рис. 4), когда ускорение

направлено вертикально вниз
и задано по величине специальными условиями движения.
Такая физическая ситуация возникает, например, в том
случае, если трос, удерживающий лифт, оборвался, но
сработало тормозное устройство, не позволяющее лифту
падать в шахте с ускорением свободного падения.
Сила тяжести, направленная вертикально вниз,
оказывается частично скомпенсированной силой трения
тормозного устройства. Понятно, что в этом
случае ускорение, с которым будет падать
лифт и кубик, находящийся в нем, будет
определяться разностью силы тяжести и
силы трения, развиваемой тормозным
устройством.

Таким образом, при движении
лифта с ускорением, вес тела,
находящегося в лифте, будет отличаться
от веса, измеренного в неподвижном лифте.
Действительно, если координатную ось
OY направить
вертикально вниз, то векторы
,
и
оказываются параллельными оси
OY, а их проекции положительными;
тогда уравнение (в векторной форме) примет вид:

(11)

Так как проекции положительны и параллельны
координатной оси, их можно заменить модулями:

(12)

Таким образом, из выражения (12) следует,
что вес тела, направление ускорения которого
совпадает с направлением ускорения свободного
падения, меньше веса покоящегося тела.
Именно этот случай показан на рисунке, где
внутри лифта размещено тело (кубик). Из
этого же выражения хорошо видно, что если
наше тело и наш лифт движутся вниз с одинаковым
ускорением, равным ускорению свободного падения,
то сила упругой реакции опоры (лифта) на тело
(кубик) отсутствует. Таким образом отсутствует
сила взаимодействия кубика с лифтом, и кубик
оказывается в состоянии
невесомости. Понятно, что это
состояние может наступить только тогда, когда
трос, на котором подвешен лифт, оборван, а тормозное
устройство не работает.

Вес и невесомость: что есть что

Понятие веса широко используется в повседневной жизни

Но, решая задачи по физике, очень важно различать вес и массу

Обозначается латинской буквой P, как и любая механическая сила, измеряется в Ньютонах. Вес – векторная физическая величина.

Не путайте вес с массой а также с силой тяжести! Это важно при решении задач. Космонавты на орбите испытывают состояние невесомости

Но не следует путать невесомость с отсутствием гравитации

Космонавты на орбите испытывают состояние невесомости. Но не следует путать невесомость с отсутствием гравитации.

Примеры проявления невесомости:

автомобиль подскакивает на ухабе и отрывается колесами от дороги;
самолет проваливается в воздушную яму;
десантник свободно падает, прежде чем раскрыть парашют;
космонавт находится в космическом корабле, который движется по орбите с выключенным двигателем.

Вес или масса изделия. Масса или вес

Много лет назад, заканчивая школу, я был полностью уверен, что при взвешивании чего либо мы определяем вес тела, и уже зная его, можем вычислить его массу, разделив полученное значение на ускорение свободного падения. Мир, в который я пришел с этими знаниями был для меня незыблемым, так как мне казалось, что за школьные годы я овладел важным фундаментальным знанием и знал что такое вес, и что такое масса.Некоторая неловкость была с единицами измерения. Вес измерялся в каких-то килограмм-силах, а масса в килограммах. Когда я приходил в магазин или на рынок, мне почему-то всё взвешивали в килограммах, а не в килограмм-силах. Было странно, но для повседневной жизни не критично.Более серьезное неудобство возникло, когда пришлось пользоваться таблицами плотности вещества. Из курса физики я знал, что плотность измеряется отношением массы тела к объёму который оно занимает. Собственно это подтверждается и единицей измерения плотности, которая приводится в каждой таблице: кг/м куб. Казалось бы ситуация предельно проста. Измеряем объём тела, умножаем его на табличное значение плотности и получаем значение массы. Для того чтобы узнать сколько тело весит это значение необходимо умножить на ускорение свободного падения.И вот тут возникла первая серьезная неприятность. Значения плотности в таблицах приведены не в массах, а в весе. Это уже был серьезный звоночек. Чтобы вычислить массу тела с использованием табличных данных, приходилось все время держать в уме, что это в расчете получается не масса, а вес, который уже отдельным действием надо приводить к массе.Извращенность физики приучала к извращенному мышлению: читаем одно, думаем о другом, пишем третье.Но даже к такой круговерти гибкое человеческое мышление адаптируется. Но вот то, что у нас международный эталон массы в один килограмм, оказался равным одной килограмм-силе, уже находится за гранью какого либо понимания.Эталон массы выполнен из платины в виде цилиндра с одинаковой высотой и диаметром: 39 мм, т.е. имеет объём 46,59 см куб.Один килограмм это 1000 грамм. Делим 1000 г на 46,59 см куб. Получаем 21,46 г/см куб.Это значение соответствует плотности платины выраженной… в ВЕСЕ!Вот с такой неразберихой наука претендует на исключительность знаний об окружающем нас мире.Чему уж тут удивляться, что многие люди просто не видят разницы между весом и массой, если даже на международном уровне такая мешанина явление обычное.Справедливости ради следует отметить, что неразбериха с массой и весом вызвана применяемыми в настоящее время единицами измерения.В международной системе СИ вес как сила должен измеряться в Ньютонах, а в обыденной практике и технических расчетах применяют килограмм-силу (кгс), которая соответствует 9,8 Н и представляет собой силу которую развивает тело массой в 1 кг и ускорением свободного падения. Поэтому когда вес измеряется в кгс, то численно он равен массе тела в кг.Поскольку переход от массы к весу должен иметь некую формульную зависимость, но которую в справочниках не приводят, то пользователь сам должен догадываться что в данном случае подразумевал составитель того или иного справочника.Не удобно, но жить можно.