Нанесение окружности, деление ее на равные части и построение многоугольников

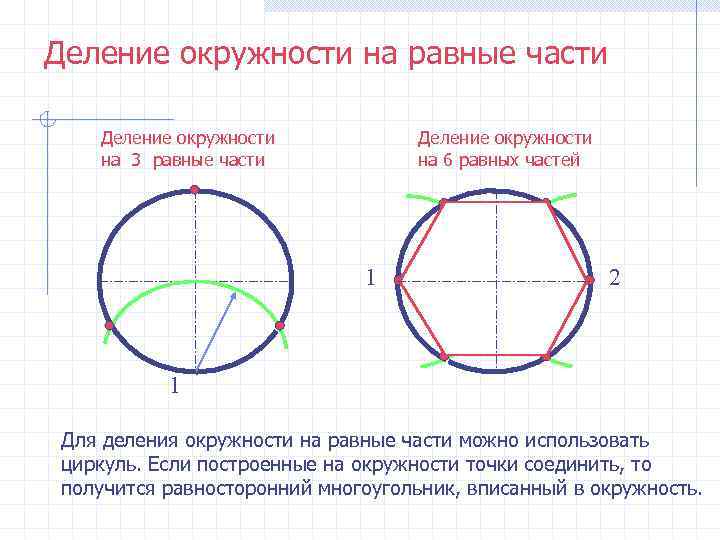
Деление на 3 и 6 частей

Чтобы правильно разделить окружность на 6 частей можно использовать свойство правильного шестиугольника, т.е. его самая длинная диагональ должна составлять две длины его стороны. Для начала циркуль необходимо растянуть на длину равную радиусу фигуры. Далее оставляя одну из ножек инструмента в любой точке окружности, второй необходимо сделать засечку, после чего повторяя манипуляции, получится сделать шесть точек, соединив которые можно получить шестиугольник (см. фото).

Соединив вершины фигуры через одну, можно получить правильный треугольник, а соответственно фигуру можно поделить на 3 равные части, а соединив все вершины и проведя через них диагонали можно разделить фигуру на 6 частей.

Деление на 4 и 8 частей

Если окружность необходимо поделить на 4 равные части, прежде всего, необходимо начертить диаметр фигуры. Это позволит получить сразу две из нужных четырех точек. Далее нужно взять циркуль, растянуть его ножки по диаметру, после чего одну из них оставить на одном из концов диаметра, а другой сделать засечки за пределами круга снизу и сверху (см. фото).

То же необходимо сделать и для другого конца диаметра. После этого полученные за пределами круга точки соединяются при помощи линейки и карандаша. Полученная линия будет вторым диаметром, который будет идти четко перпендикулярно первому, в результате чего фигура будет поделена на 4 части. Для того чтобы получить, например, 8 равных частей, полученные прямые углы можно разделить пополам и провести через них диагонали.

Деление окружности на три равные части. Устанавливают угольник с углами 30 и 60° большим катетом параллельно одной из центровых линий. Вдоль гипотенузы из точки 1
(первое деление) проводят хорду (рис. 2.11, а
), получая второе деление – точку 2. Перевернув угольник и проведя вторую хорду, получают третье деление – точку 3
(рис. 2.11, б
). Соединив точки 2 и 3; 3
и 1
прямыми, получают равносторонний треугольник.

Рис. 2.11.

а, б – с
помощью угольника; в
– с помощью циркуля

Ту же задачу можно решить с помощью циркуля. Поставив опорную ножку циркуля в нижний или верхний конец диаметра (рис. 2.11, в
), описывают дугу, радиус которой равен радиусу окружности. Получают первое и второе деления. Третье деление находится на противоположном конце диаметра.

Деление окружности на пять, десять и семь равных частей

В плашке (рис. 56, а) имеется пять отверстий, равномерно расположенных по окружности. Выполняя чертеж плашки (рис. 56, в), необходимо разделить окружность на пять равных частей. Через намеченный центр О (рис. 56, б) с помощью рейсшины и угольника проводят осевые линии и из точки О циркулем описывают окружность заданного диаметра. Из точки А радиусом R, равным радиусу данной окружности, проводят дугу, которая пересечет окружность в точке n. Из точки n опускают перпендикуляр на горизонтальную осевую линию, получают точку С. Из точки С радиусом R₁ равным расстоянию от точки С до точки 1, проводят дугу, которая пересечет горизонтальную осевую линию в точке т. Из точки 1 радиусом R₂, равным расстоянию от точки 1 до точки т, проводят дугу, пересекающую окружность в точке 2. Дуга 12 является 1/5 длины окружности. Точки 3, 4 и 5 находят, откладывая циркулем отрезки, равные m1.

Рис. 56

Рис. 57

Рис. 58

Рис. 59

Деталь ’’звездочка” (рис. 57, а) имеет 10 одинаковых элементов, равномерно расположенных по окружности. Чтобы выполнить чертеж звездочки (рис. 57, в), следует окружность разделить на 10 равных частей. В этом случае следует применить то же построение, что и при делении окружности на пять частей (см. рис. 56, б). Отрезок п₁будет равняться хорде, которая делит окружность на 10 равных частей.

На рис. 58, а изображен шкив, а на рис. 58, в — чертеж шкива, где окружность разделена на семь равных частей.

Деление окружности на семь равных частей показано на рис. 58, б. Из точки А проводится вспомогательная дуга радиусом R,равным радиусу данной окружности, которая пересечет окружность в точке п. Из точки п опускают перпендикуляр на горизонтальную осевую линию. Из точки 1 радиусом, равным отрезку nс, делают по окружности семь засечек и получают семь искомых точек.

Деление окружности на любое число равных частей. С достаточной точностью можно делить окружность на любое число равных частей, пользуясь таблицей коэффициентов для подсчета длины хорды (табл. 10).

Зная, на сколько частей (n) следует разделить окружность, находят по таблице соответствующий коэффициент к. При умножении коэффициента к на диаметр окружности D получают длину хорды l, которую циркулем откладывают на окружности n раз.

При построении чертежа кольца (рис. 59, а) необходимо окружность диаметра D= 142 мм разделить на 32 равные части. Зная число n, по таблице находим коэффициент к = 0,098. Подсчитав длину хорды I = Dk= 142*0,098 — 13,9 мм, циркулем откладывают ее 32 раза (рис. 59, би в).

Таблица 10

Значение коэффициента k при делении окружности на n равных частей

n	к	n	к	n	к
7	0,434	17	0,184	27	0,116
8	0,383	18	0,174	28	0,112
9	0,342	19	0,165	29	0,108
10	0,309	20	0,156	30	0,104
И	0,282	21	0,149	31	0,101
12	0,259	22	0,142	32	0,098
13	0,239	23	0,136	33	0,095
14	0,223	24	0,130	34	0,092
15	0,208	25	0,125	35	0,900
16	0,195	26	0,120	36	0,087

Примеры и образцы решения задач:

Решение задач по инженерной графике
Решение задач по начертательной геометрии

Услуги по выполнению чертежей:

Заказать чертежи
Помощь с чертежами
Заказать чертеж в компасе
Заказать чертеж в автокаде
Заказать чертежи по инженерной графике
Заказать чертежи по начертательной геометрии
Заказать черчение

Учебные лекции:

Инженерная графика
Начертательная геометрия
Оформление чертежей
Чертеж общего вида и сборочный чертеж
Техническое рисование
Машиностроительные чертежи
Геометрические построения
Сопряжение линий
Коробовые кривые линии
Построение уклона и конусности
Лекальные кривые
Параллельность и перпендикулярность
Методы преобразования ортогональных проекций
Поверхности
Способы проецирования
Метрические задачи
Способы преобразования чертежа
Кривые линии
Кривые поверхности
Трёхгранник Френе
Проецирование многогранников
Проецирование тел вращения
Развёртывание поверхностей
Проекционное черчение
Проецирование
Проецирование точки
Проецирование отрезка прямой линии
Проецирование плоских фигур
Способы преобразования проекций
Аксонометрическое проецирование
Проекции геометрических тел
Сечение геометрических тел плоскостями и развертки их поверхностей
Взаимное пересечение поверхностей тел
Сечение полых моделей
Разрезы
Требования к чертежам деталей
Допуски и посадки
Шероховатость поверхностей и обозначение покрытий
Разъемные и неразъемные соединения деталей
Передачи и их элементы

§ 8. Построение углов. Деление окружности на равные части

Построение прямых углов. Угол 90 целесообразно строить при помощи рейсшины и угольника (рис. 53).

Рис. 53. Построение прямых углов

Построение тупых и острых углов. Рациональные способы построения углов 120, 30 и 150; 60 и 120; 15 и 165; 75 и 105; 45 и 135 приведены на рис. 54.

Рис. 54. Построение тупых и острых углов

Деление угла пополам. Из вершины угла описывают дугу окружности произвольного радиуса (рис. 55). Из точек m и n пересечения дуги со сторонами угла раствором циркуля, большим половины дуги mn, делают две пересекающиеся засечки (точка 1).

Полученную точку 1 соединяют прямой с вершиной угла.

Рис. 55.

Деление отрезка прямой пополам. Из концов заданного отрезка раствором циркуля, большим половины его длины, описывают дуги (рис. 56). Прямая, соединяющая полученные точки m и n, делит отрезок на две равные части и перпендикулярна ему.

Рис. 56.

Деление прямого угла на три равные части. Из вершины прямого угла описывают дугу окружности произвольного радиуса (рис. 57). Не меняя раствора циркуля, делают засечки из точек пересечения дуги со сторонами угла. Полученные точки тип соединяют прямыми с вершиной угла.

Рис. 57.

Деление окружности на три равные части. Угольник с углами 30 и 60 устанавливают так, чтобы большой катет был параллелен одной из центровых линий. Вдоль гипотенузы из точки 1 (первое деление) проводят хорду, получают второе деление (рис. 58, а). Перевернув угольник и проведя вторую хорду, получают третье деление (рис. 58, б). Соединив точки 2 и 3 прямой, получают равносторонний треугольник.

Ту же задачу можно решить с помощью циркуля. Поставив опорную ножку циркуля в конечную точку диаметра (рис. 58, в), описывают дугу радиусом, равным радиусу R окружности. Получают первое и второе деление (точки 1 и 2). Третье деление (точка 3) находится на противоположном конце диаметра.

Рис. 58.

Деление окружности на шесть равных частей. Раствор циркуля устанавливают равным радиусу R окружности (рис.

()

Рис. 59. Деление окружности на шесть равных частей при помощи циркуля

Рис. 60. Деление окружности на шесть равных частей при помощи угольника

Рис. 61. Деление окружности на восемь равных частей

Рис. 62. Определение центра дуги

Упражнение 32

Разделите отрезок прямой АВ на четыре равные части.

Упражнение 33

Разделите тупой угол на четыре равные части.

Упражнение 34

При помощи угольника и линейки разделите окружность на 12 равных частей. То же самое сделайте с помощью циркуля.

Упражнение 35

Подсчитайте, чему равна длина хорды при делении окружности диаметром 100 мм на 15 равных частей.

Нахождение центра дуги и определение величины радиуса

Задана дуга окружности, центр и радиус которой неизвестны.

Для их определения нужно провести две непараллельные хорды (рис. 2.15, а
) и восставить перпендикуляры к серединам хорд (рис. 2.15, б
). Центр О
дуги находится на пересечении этих перпендикуляров.

Рис. 2.15.

Сопряжения

При выполнении машиностроительных чертежей, а также при разметке заготовок деталей на производстве часто приходится плавно соединять прямые линии с дугами окружностей или дугу окружности с дугами других окружностей, т.е. выполнять сопряжение.

Сопряжением
называют плавный переход прямой в дугу окружности или одной дуги в другую.

Для построения сопряжений надо знать величину радиуса сопряжений, найти центры, из которых проводят дуги, т.е. центры сопряжений
(рис. 2.16). Затем нужно найти точки, в которых одна линия переходит в другую, т.е. точки сопряжений.
При построении чертежа сопрягающиеся линии нужно доводить точно до этих точек. Точка сопряжения дуги окружности и прямой лежит на перпендикуляре, опущенном из центра дуги на сопрягаемую прямую (рис. 2.17, а
), или на линии, соединяющей центры сопрягаемых дуг (рис. 2.17, б
). Следовательно, для построения любого сопряжения дугой заданного радиуса нужно найти центр сопряжения
и точку
(точки
) сопряжения.

Рис. 2.16.

Рис. 2.17.

Сопряжение двух пересекающихся прямых дугой заданного радиуса. Даны пересекающиеся под прямым, острым и тупым углами прямые линии (рис. 2.18, а
). Нужно построить сопряжения этих прямых дугой заданного радиуса R.

Рис. 2.18.

Для всех трех случаев можно применять следующее построение.

1. Находят точку О
– центр сопряжения, который должен лежать на расстоянии R
от сторон угла, т.е. в точке пересечения прямых, проходящих параллельно сторонам угла на расстоянии R
от них (рис. 2.18, б
).

Для проведения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, равным R,
делают засечки и к ним проводят касательные (рис. 2.18, б
).

2. Находят точки сопряжений (рис. 2.18, в). Для этого из точки О
опускают перпендикуляры на заданные прямые.
3. Из точки О, как из центра, описывают дугу заданного радиуса R
между точками сопряжений (рис. 2.18, в).

Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.

Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами
R.

Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром
D.

Части окружностей называются дугами
.

Прямая СD, соединяющая две точки на окружности, называется хордой
.

Прямая МN,которая имеет только одну общую точку с окружностью называется касательной
.

Часть круга, ограниченная хордой СD и дугой, называется сигментом
.

Часть круга, ограниченная двумя радиусами и дугой, называется сектором
.

Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности
.

Угол, образованный двумя радиусами КОА, называется центральным углом
.

Два взаимно перпендикулярных радиуса
составляют угол в 90 0 и ограничивают 1/4 окружности.

Деление окружности на части

Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.

3. Не много из истории

С делением окружности неразрывно связано построение
правильных многоугольников. Они встречаются в древнейших орнаментах у всех
народов. Люди уже тогда оценивали их красоту. Кроме того, они видели эти фигуры
в природе. Например, пятиугольник встречается в очертаниях минералов, цветов,
плодов, в форме некоторых морских животных, шестиугольник просматривается в
пчелиных сотах и т.д.
В «Десяти книгах
о зодчестве» римского архитектора Витрувия (жившего примерно в 63-14 гг. до н.
э.) говорится, что городские стены должны иметь в плане вид правильного
многоугольника, а башни крепости «следует делать круглыми или многоугольными,
ибо четырехугольник скорее разрушается осадными орудиями»
Планировка городов, которую предлагал Витрувий представляла собой защиту
от 8 главных ветров и 16 второстепенных.. для построения восьмиугольника
Витрувий предлагал применить деления пополам сторон квадрата, вписанного в
окружность.
Правильный
шестиугольник явился предметом исследования великого немецкого астронома и
математика Иоганна Кеплера (1571-1630), о котором он рассказывает в своей книге
«Новогодний подарок, или о шестиугольных снежинках». Рассуждая о причинах того,
почему снежинки имеют шестиугольную форму, он отмечает: «…плоскость можно
покрыть без зазоров лишь следующими фигурами: равносторонними треугольниками,
квадратами и правильными шестиугольниками. Среди этих фигур правильный
шестиугольник покрывает большую площадь»
Одним из наиболее
известных ученых, занимавшихся геометрическими построениями, был великий
художник и математик Альбрехт Дюрер (1471-1528), который посвятил им
значительную часть своей книги «Руководства…». Он предложил правила построения
правильных многоугольников с 3, 4, 5…16-ю сторонами. Методы деления были не
универсальны, в каждом конкретном случае используется индивидуальный прием.

4. Где встречается?

В строительстве
широко применяли деление окружности на равные части. Одним из примеров может
служить величественный памятник готической архитектуры – Нотр–Дам де Пари или
Собор Парижской Богоматери (30
метров в длину, 108 – в ширину) который находится в
Париже, на острове Сити. Его строили 94 года. Фасад Собора украшает
удивительный витраж 18 века. Этот витраж в архитектуре называется «роза».
Диаметр розы собора Собор Парижской Богоматери12 метров 90 см.
В
декоративно-прикладном искусстве дизайнеры, ювелиры с успехом применяли деление
окружности, создавая прекрасные произведения: ордена, медали, монеты, ювелирные
изделия
Ювелирная огранка