Основные геометрические фигуры

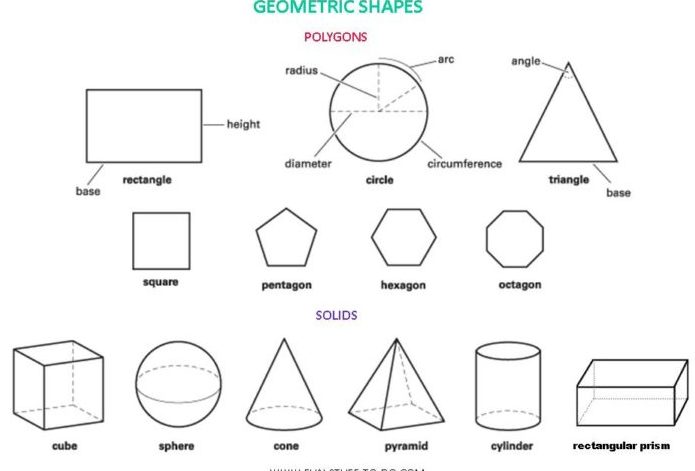
Что такое 10-сторонний многоугольник?

В геометрии десятиугольник (от греч. δέκα déka и γωνία gonía, «десять углов») — десятиугольный многоугольник или 10-угольник. Общая сумма внутренних углов простого десятиугольника составляет 1440 °.

Что означает базовая форма?

Основные формы включают квадрат, круг и треугольник. У вас может быть нос в форме лыжного склона. Когда вы восхищаетесь чьей-то формой, вы восхищаетесь их формой или телом. Когда вы не в форме или обещаете вернуться в форму, вы используете форму для обозначения своей физической выносливости или общего состояния здоровья.

Сколько основных форм существует в искусстве? Есть три основные формы архетипы, в которые может быть вписана любая форма: куб, цилиндр и сфера. В основе этих форм лежат две простые геометрические фигуры: квадрат и эллипс. Научившись точно рисовать и комбинировать их, вы сможете построить любой наблюдаемый или воображаемый объект.

Ромб и алмаз — одно и то же? Алмаз представляет собой четырехугольник, двумерную плоскую фигуру с четырьмя замкнутыми прямыми сторонами. Но алмаз также относится к категории ромбов, потому что он имеет четыре равные стороны и его противоположные углы равны. И, поскольку его противоположные стороны параллельны, он также считается параллелограммом.

Сложные модели

В сложной геометрии выделяют фигуры с пространственным, плоским и объемным наполнением. Существует понятие геометрического тела, 3D-моделирование и проекция.

Определение тела и пространства

Геометрическое тело (ГТ) представляет часть пространства, отделенное замкнутой поверхностью наружной границы. Это понятие относится к компактному множеству точек, а две из них соединяют отрезком, проходящим внутри границы тела. Внешняя граница ГТ является его гранью, которых может быть несколько. Множество плоских граней определяет вершины и ребра ГТ. Все геометрические тела делятся на многогранники и тела вращения.

Тела вращения — объемные тела, образующиеся из-за вращения плоской фигуры, ограниченной кривой, вокруг оси. Эта ось расположена в той же плоскости. При вращении контуров фигур вокруг собственной оси возникает поверхность вращения, а если вращать заполненные контуры — возникают объекты (шар).

Шар представляет множество точек, расположенных от данной точки на небольшом пространстве. Точка является центром шара, а расстояние ограничено радиусом.

В сферу геометрии входят плоские (двухмерные) и объемные пространственные фигуры (трехмерные).

Существуют двухмерные фигуры (2D), представленные углом, многоугольником, четырехугольником, окружностью, кругом, эллипсом и овалом. Объекты 3D выделены двугранным или многогранным углом. Среди них известны призма, параллелепипед, куб, антипризма, пирамида, тетраэдр икосаэдр, бипирамида, геоид, эллипсоид, сфера шар и другие. Плоские фигуры изучает планиметрия, а объемные — стереометрия.

Объемные фигуры:

• Шар.
• Конус.
• Параллелепипед.
• Цилиндр.
• Сфера.

Конус образуется из треугольника с прямыми углами, при вращении его вокруг одного из катетов. Тороид возникает из замкнутой плоскости (окружности), вращающейся вокруг прямой и не пересекающей ее. Многогранник называется полиэдр, представляет замкнутую поверхность, состоящую из многоугольников.

Виды многогранников:

• Тетраэдер (четырехгранник). Это правильный треугольник.
• Куб (гексаэдр). Грани являются квадратом.
• Октаэдр. Имеется шесть вершин и восемь граней.
• Икосаэдр. Равносторонние треугольники являются гранями. Имеется 12 граней и 12 вершин.
• Додекаэдр. Правильные шестиугольники, имеется 12 граней, 20 вершин.

Познавательные игрушки детям

Геометрия является наукой, которой можно знакомить детей с раннего возраста. Лучше распечатать картинки, геометрические фигуры для детей, затем нарисовать их вместе на чистом листе. Малышу первого года подобное занятие будет не очень интересным и понятным, а у дошкольника вызовет интерес, особенно если объекты изучения будут разноцветными или в необычном исполнении.

Основной материал для обучения детей:

• Яркие карточки с основными фигурами, формами. Шаблоны будут наглядным пособием перед школой.
• Раскраски, прописи, рабочая тетрадь. На каждой странице тетради представлены простейшие графические упражнения и задания. Выполняя их, малыш познакомится с геометрией и узнает названия фигур.
• Специальная детская литература.

Увлекательные, забавные, задорные стихи «Веселая геометрия для малышей» помогут детям быстро познакомиться и усвоить много важной информации о фигурах и размерах предметов. Веселые стишки помогут юному читателю соотнести малопонятные геометрические знания с обыденными предметами обихода

Например, в женской юбке представлена трапеция, в блюдце— круг, а в трубе цилиндр.

Ближе к дошкольному возрасту переходят на объемные фигуры, кубики, конусы, кольца и цилиндры. В школьном возрасте знания накопятся, и дети будут осознанно различать равнобедренный, равносторонний треугольник, три понятия: луч, отрезок, окружность.

Раздел математики геометрия изучает пространственные отношения и формы. Фигура как понятие, рассмотренное во всех учебниках геометрии, является пространственной формой.

Геометрию можно обнаружить везде — в любых окружающих предметах. Это современные здания, архитектурные строения, формы, космическая станция, интерьер квартиры, подводные лодки.

Математические знания являются профессионально важными для современных специальностей: дизайнеров и конструкторов, рабочих и ученых. Без знания основ геометрии невозможно построить здание или отремонтировать квартиру.

Простейшие виды фигур

Две основные фигуры — это точка и линия. Скопление точек и линий образует различные геометрические фигуры. Каждая из них индивидуальна, отличается своими параметрами, их формы очень разнообразны. Фигуры бывают простыми и сложными, плоскими и объёмными.

Точка

Точка — это самый минимальный, но в то же время самый главный объект в геометрии. Это самая малая геометрическая фигура, но именно она необходима для построения других фигур на плоскости и является основой для всех других фигур. Она не содержит таких свойств, как длина, высота, объём, площадь, не имеет измерительных особенностей и характеристик

Важно только то, где она расположена. Обозначается точка заглавной буквой латинского алфавита либо числом

Например, A, B, C или 1, 2, 3.

Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.

Самыми простейшими фигурами являются луч и отрезок.

• Луч — часть прямой, у которой есть начальная точка, но нет конца. Это продолжение в одну сторону.
• Отрезок — составная часть прямой, которая ограничена двумя точками. Он имеет начало и конец, поэтому измеряется. Длину отрезка можно определить, измерив расстояние между его концами.

Линия

Линия образуется из множества точек, последовательно расположенных друг за другом и соединённых между собой. Линии бывают замкнутыми и разомкнутыми, прямыми и кривыми, а также ломаными. 

• Замкнутая — когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
• Разомкнутая — когда начало и окончание линии не соединены.
• Прямая — непрерывная линия без изменений.
• Кривая — отличная от прямой линии.
• Ломаная — когда соединены отрезки не под углом 180 градусов. 

Через одну точку можно провести бесконечное число линий, а через две — только одну прямую и множество кривых.

Как называются двухмерные фигуры?

Основные типы 2D-фигур: круг, треугольник, квадрат, прямоугольник, пятиугольник, четырехугольник, шестиугольник, восьмиугольник и т. д.. Кроме круга, все фигуры считаются многоугольниками, у которых есть стороны.

Как называется фигура с 4 сторонами? Определение: Четырехугольник представляет собой многоугольник с 4 сторонами. Диагональ четырехугольника — это отрезок, концы которого лежат на противоположных вершинах четырехугольника. … Определение: Параллелограмм – это четырехугольник, у которого обе пары противоположных сторон параллельны.

Как по-другому называются основные формы?

Синонимы форм – Тезаурус WordHippo. … Какое другое слово для формы?

форма	понять
контур	контуры
описания	контур
рама	профиль
Структура	симметрия

Является ли звезда геометрической фигурой? По геометрическому определению звезда правильный многоугольник: простой или сложный. Многоугольник – любая двумерная фигура, образованная прямыми линиями и замкнутая. Правильный многоугольник – многоугольник, все стороны которого имеют одинаковую длину (равносторонний) и все углы которого одинаковы (равноугольный).

Геометрические фигуры двухмерные или трехмерные?

Геометрия – это изучение форм. Он широко подразделяется на два типа: плоская геометрия, называемая 2D-формами, и сплошная геометрия, называемая трехмерными фигурами. … Другими словами, плоский объект, имеющий только длину и ширину, представляет собой двумерную форму. Прямые или изогнутые линии составляют стороны этой формы.

Как определить геометрическую фигуру?

Как учить геометрические фигуры?

Где вы находите большинство геометрических фигур, приведите примеры? Геометрические фигуры повсюду. Куда бы вы ни посмотрели, почти все состоит из двухмерных (2D) и трехмерных (3D) геометрических фигур. … Некоторые реальные примеры квадратов:

• квадратные резиновые штампы.
• квадратная плитка на полу.
• квадратные бумажные салфетки.
• шахматные доски.
• клавиши виртуальной клавиатуры.

Общая характеристика

Предметы в геометрическом изображении состоят из отдельных частей: точек, линий, лучей, отрезков и вершин. Отдельно взятый предмет имеет свое предназначение.

Основные понятия о составляющих

Когда все точки фигуры принадлежат одной плоскости, она является плоской. К ней относятся отрезок, прямоугольник. Существуют геометрические объекты, не являющиеся разновидностью плоскости, — куб, шар, пирамида, призма.

Минимальным объектом геометрии является точка. Определение того, какой она должна быть известно из школьного математического курса. Учебник характеризует ее как объект, не имеющий измерительных особенностей. Точка (Т) не содержит стандартных свойств: высоты, длины, радиуса, важным является только ее расположение. Обозначается числом или большой заглавной буквой. Например, точка называется D, E, F или 1, 2, 3. Несколько точек бывают отмечены разными цветами или буквами для удобного различия.

Линия состоит из множества точек. Измеряется длина этого составляющего объекта и обозначается маленькими буквами (abc).

Виды линий:

• Замкнутая. Когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
• Разомкнутая. Начало и окончание не соединяются.
• Прямая. Обозначается буквой а или b.
• Ломаная. Заключается в соединенных отрезках не под углом 180 градусов. Линия обозначается перечислением всех вершин.
• Кривая.Отличная от прямой линии.

Существуют подвиды прямой линии: пересекающиеся, содержащие общую точку и когда две прямые линии соединяются в одной точке.

Луч в математике представляет часть прямой, имеющей начальную точку, но не имеющую конец. Это продолжение в одну сторону. Если Т разделяет линию пополам — получается два луча. Лучевые линии совпадают, когда расположены на одной прямой, начинаются в точке или направляются в одну сторону.

Отрезок представляет составную часть прямой, ограниченной двумя точками — она имеет начало и конец, поэтому измеряется. Длина отрезка представляет расстояние между его первой и последней точками. Через одну Т проводится бесконечное число линий, а через две — кривые и только одна прямая.

Стандартные объекты

К основным фигурам геометрии на плоскости относятся прямоугольник, треугольник, квадрат, многоугольник и круг. Прямоугольник выглядит как фигура, состоящая из четырех сторон и четырех прямых углов (ПУ). Противоположные стороны равны между собой. В математике прямоугольник обозначается четырьмя латинским заглавными буквами. Все ПУ расположены под 90 градусов. Прямоугольник с равными, одинаковыми сторонами называется квадратом.

Фигура, имеющая 3 стороны и столько же углов (вершин), называется треугольником. Существует классификация этой фигуры по типу У.

Виды треугольника в зависимости от угла (У):

• Прямой. Один У будет прямым, два — менее 90 градусов.
• Острый. Градусная мера больше 0, но меньше 90 гр.
• Тупой. Один У тупой, два других будут острыми.

Радиус круга — промежуток от середины окружности до любой ее точки. Диаметр — это отрезок, соединяющий две точки окружности, проходящий через ее середину.

Параллелепипед — это призма, у которой основанием является параллелограмм. Когда все ребра параллелепипеда равны, получается куб.

Многогранная фигура, у которой одна грань является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной, называется пирамидой.

Семиугольник (гептагон) — это многоугольник с 7 углами. Многоугольник представляет замкнутую ломанную линию.

Основные фигуры перечислены, но геометрия включает еще сложные объекты, использующиеся в различных областях жизни.

Что такое отрезок?

 Давайте схематично изобразим удава. Сначала отметим две точки – голова и хвост (начало и конец). После соединим эти точки.

Получается, что схематично изображая удава, начертили еще одну геометрическую фигуру, которая называется отрезком. Давайте сформулируем определение:

Отрезок–это фигура на прямой, ограниченная двумя точками. Точки называются концами отрезка и обозначаются заглавными буквами латиницы.

Произносится: отрезок ТМ.

Если при наложении концы отрезков совпадают, то такие отрезки называют равными.

Значит, АВ=КМ

А что такое единичный отрезок, где используется?

Давайте вернемся к мультфильму. Вспомните момент, когда удава очень волновал его рост (длина). Друзья не растерялись, нашли способ его измерять. Сначала его измеряли обезьянками, потом слонами, наконец, попугаями.

 Но каждый раз длина удава была разной только потому, что друзья очень отличались своими размерами. При измерении длины удава, каждый друг выступил в роли единичного отрезка, величины, в которой измерялся предмет (в слонах, обезьянах, попугаях). Так как попугай имел самый маленький размер, то длина удава в попугаях оказалась самой большой – 38 попугаев. Сформулируем определение:

Единичный отрезок – выбранная единица для измерения чего-либо.

Возьмем линейку длиной 20 см. На ней можно увидеть штрихи, делящие линейку на одинаковые кусочки, которые называют делениями. Из них состоит шкала. За единицу измерения принят отрезок длиной 1 см (единичный), и таких единиц измерения на линейке 20 штук.

Для изучения следующего понятия необходимо схематически начертить линейку. Для этого чертим луч, указываем направление луча стрелочкой, наносимделения:

Точка В, с соответствующимчисловым значением 0. Следующая точка С, с числовым значением 1. Получается, отрезок ВС считается единичным, его длина принимается за единицу измерения. Все имеющиеся точки расположены на расстоянии единичного отрезка.

Луч с нанесенным единичным отрезком, направлением, называют координатным лучом, координатной прямой.

Каждая точка на координатном луче имеет соответствующее числовое значение – координату точки.

Точке Р соответствует числовое значение 5.

Обозначается на письме: Р (5).

Произносится: координата точки Р – 5

Постарайтесь запомнить эти понятия, чтобы избежать трудностей с определением координат точек!

Фигура, которую мы рассмотрим, состоит из точки, лучей.

Давайте отметим начало двух лучей точкой.

Полученная фигура называется углом.

Угол– геометрическая фигура, состоящая из точки и выходящих из неё лучей.

Что такое круг?

Круг – это область внутри окружности, учитывающая саму окружность.

Точка О называется центром круга.

Если центр окружности соединить отрезком с точкой окружности, то получим радиус. Радиус принято обозначать буквой латиницы–R.

 Рассмотрим на примере что такое радиус: отрезок ОВ соединяет центр окружности и точку, лежащую на окружности, поэтому онявляется радиусом. ОВ=R.

Протяженность от центра до любой точки окружности одинакова, все радиусы одной окружности равны. ОС=ОВ=R.

Если отрезком, проведенным через центр окружности соединить две точки окружности, то получим диаметр окружности.

Диаметр окружности – это длина отрезка РК, диаметр обозначается буквой латиницы – D. Значит, РК= D.

 На рисунке видно, что диаметр состоит из двух радиусов, то есть D=R+R=2R.

 И последнее, часть окружности между любыми точками окружности, называется дугой окружности.

Основные величины и их формулы

Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.

Периметр

Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:

На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.

Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.

Обозначается заглавной латинской P.

Площадь

Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра. Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь. 

‍

На рисунке площади фигур окрашены различными цветами.

Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д. S (square) — знак площади.

Вычисление периметра и площади

Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.

• Квадрат: периметр = 4 * сторона.
• Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.
• Неправильный многоугольник: периметр = сумме всех сторон многоугольника.
• Круг: длина окружности = 2 * π * радиус = π * диаметр (где π – это число пи (константа, примерно равная 3,14), радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности, диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности).

Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:

• Параллелограмм: площадь = основание * высота
• Квадрат: площадь = сторона 1 * сторона 2
• Треугольник: площадь = ½ * основание * высота
• Круг: площадь = π * радиус² (где радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя).

Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа iSmart поможет вашему ребёнок изучить основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:

• интерактивные задания больше похожи на игру;
• их можно отрабатывать многократно и они не будут повторяться;
• платформа сформирует индивидуальную траекторию обучения на основе диагностики знаний;
• достаточно всего 20 минут занятий в день, чтобы в короткий срок увидеть прогресс в обучении.

Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение и поведенческий анализ.

Образовательная платформа iSmart предлагает подготовку к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.

Сколько существует геометрических фигур?

Существуют два типа геометрических фигуры, классифицируемые как: Двумерные: это 2D-формы, которые имеют только ось x и ось y. Это плоские структуры с 2 измерениями. Например, треугольник, квадрат, прямоугольник и т. д.

Также Каковы 20 основных форм? Основные имена фигур

• Нонагон.
• Октагон.
• Семиугольник.
• Шестиугольник.
• Треугольник.
• Неравносторонний треугольник.
• Прямоугольный треугольник.
• Параллелограмм.

Как вы определяете формы?

Каковы наиболее распространенные формы? Чай квадрат, круг и треугольник являются самыми основными формами на Земле, поддерживающими как синтетические, так и натуральные конструкции.

Что такое вершина и стороны угла?

Точка называется вершиной угла, лучи– сторонами угла. Обозначают строчными, заглавными буквами латиницы (отметив на сторонах дополнительные точки). Для письменного обозначенияиспользуется специальный знак ∠.

Записывается, читается:∠β – угол бета,∠BAС – угол BAС.

Углы равны, если при наложении они совпадают.

Мы наложили ∠BAС на ∠ β,при совмещении, у них совпали (полностью совместились) вершины, стороны углов. Значит ∠BAС=∠ β.

Бывают случаи, когда източки выходят два луча в противоположные стороны, образуя при этом прямую линию. Например:

Полученная фигура называется развернутым углом.

Развернутый угол – фигура, стороны которой, дополняя друг друга, создают прямую линию. Градусная мера угласоставляет 180 ˚.

Все углы принято измерять градусами. Градус–единица измерения углов, составляет 1/180 часть развернутого угла. Для письменного обозначения градуса используется специальный символ – ˚.

Получается, что∠ α=180 ˚.

Читается как: градусная мера развернутого угла альфа равна 180 градусам.

Если такой угол разделить пополам, то получим 2 равнозначных угла.

Рассмотрим развернутый ∠ВАС. Луч АО делит ∠ВАС пополам, чтобы узнать градусную меру полученных углов, необходимо градусную меру развернутого угла, поделить пополам (180:2=90). Получается, что ∠ОАС и ∠ВАО имеют градусную меру равную 90 ˚, называются прямыми углами.

Прямым углом называют половину развернутого угла, градусная мера которого составляет 90 ˚

Ну, а теперь, можете попросить у родителей чашку горячего чая. Ведь для изучения следующего определения, будем использовать вкусный, ароматный бублик.

Бублик – лакомство, знакомое с самого детства. Но вряд ли кто-то из вас задумывался какую форму имеет любимая выпечка? Если рассматриватьс геометрической точки зрения, то бублик представляетзамкнутую линию теста, все точки которой лежат на одинаковом расстоянии от центра изделия. В геометрии такая фигура называется окружностью.

Что такое точка?

Как только маленький ребенок берет в ручки карандаш, он уже замечательно умеет рисовать геометрическую фигуру. Какую? – удивитесь вы. Это точка.

Точка – наименьшая, простейшая фигура геометрии, никак не измеряется.

 И строить её умеет даже маленький ребенок.

Обозначать точки в математике, принято большими буквами латиницы.

Произносится:точка А, точка В, точка С.

Следующее понятие, которое мы рассмотрим, знакомо каждому с самого детства. Нет ничего проще, чем нарисовать прямую линию. Многие успешно рисовали их на новых обоях, мебели. А оказывается – она одна из основных фигур геометрии.