Относительное положение двух окружностей
Концентрические и эксцентрические круги. Два круга называются концентрическими, когда они имеют один общий центр, и эксцентрическими, когда из центры не совпадают.
На чертеже 96 представлены круги концентрические и на чертежах 97, 98, 99, 100 и 101 круги эксцентрические.
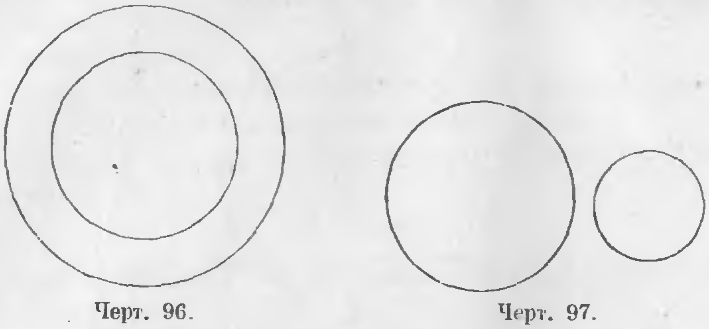
Внешние и внутренние круги. Круги называются внешними, когда все точки одного лежат вне площади другого круга, и внутренними, когда все точки одного лежат внутри площади другого круга.
На чертежах 97 и 99 изображены круги внешние, на чертежах 96, 98 и 100 круги внутренние.
Касательные окружности. Окружности называются касательными, когда они имеют одну общую точку.
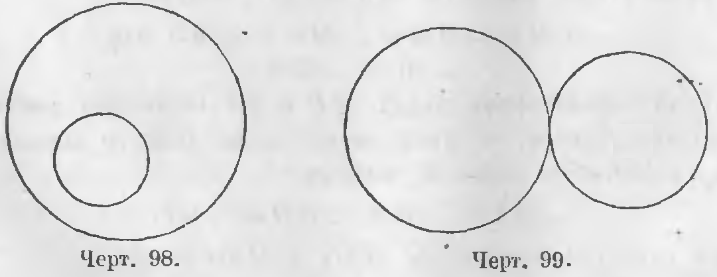
Общая точка двух касательных окружностей называется их точкой соприкосновения. Соприкосновение называется внешним, когда два круга, имея общую точку, лежат один вне другого, и внутренним, когда один круг лежит внутри другого. На черт. 99 имеем случай внешнего, а на чертеже 100 случай внутреннего соприкосновения.
Пересекающиеся окружности. Окружности называются пересекающимися, когда они имеют две общие точки (черт. 101).
Линия центров есть отрезок, соединяющий центры двух кругов.
Теорема 71. Две окружности, имеющие общую точку на линии центров, другой общей точки иметь не могут.
Дано. Две окружности с центрами O и O’ имеют общую точку A (черт. 102).
Требуется доказать, что другой общей точки у них нет.
Доказательство. Положим, существует другая общая точка B, следовательно,
OB = OA и O’B = O’A.
Складывая эти равенства, мы имели бы
OB + O’B = OA + O’A или
OB + O’B = OO’
равенство несообразное, ибо ломаная не может равняться прямой.
Итак, другой общей точки быть не может (ЧТД).
Теорема 72. Две окружности, имеющие одну общую точку вне линии центров, имеют и другую общую точку по другую сторону линии центров.
Дано. Две окружности, центры которых O и O’, имеют общую точку A вне отрезка OO’ (черт. 103), соединяющей центры.
Требуется доказать, что существует и другая общая точка по другую сторону центров.
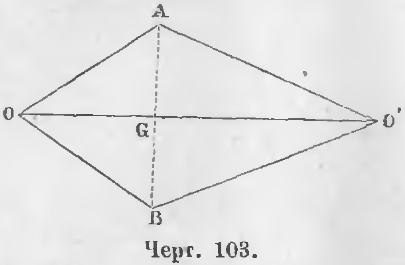
Доказательство. Из точки A опустим на линию центров перпендикуляр AG и на продолжении его отложим отрезок BG, равный AG.
Докажем, что точка B будет другая общая точка. Точка B лежит на окружности O, ибо AO = BO как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’. Точка B лежит на окружности O’, ибо AO’ = BO’ как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’, следовательно, точка B есть другая общая точка (ЧТД).
Теорема 73. Если две окружности пересекаются в двух точках, то линия центров перпендикулярна и делит пополам хорду, соединяющую точки пересечения.
Дано. Точки A и B есть точки пересечения (черт. 104) двух окружностей.
Требуется доказать, что AG = BG и AB ⊥ OO’.
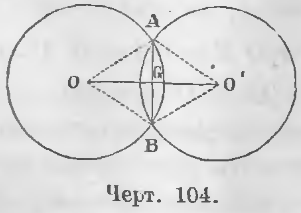
Доказательство. Треугольники OAO’ и OBO’ равны, ибо OO’ сторона общая.
OA = OB как радиусы окружности O.
O’A = O’B как радиусы окружности O’.
Следовательно,
∠AOO’ = ∠BOO’
Треугольники AOG и BOG равны, ибо OG сторона общая, AO = BO как радиусы, ∠AOG = ∠BOG по доказанному. Следовательно, AG = BG (хорда AB делится линией центров пополам), ∠AGO = ∠BGO (хорда AB перпендикулярна к линии центров).
Таким образом, хорда AB делится пополам и перпендикулярна к линии центров OO’ (ЧТД).
Касательные прямые и бильярд
Прицеливание удара в бильярде. Направление удара от битка (шар B) выбирается так, чтобы точка касания совпадала с точкой пересечения прямой, проходящей через центр лузы и центр прицельного шара. В этом случае прицельный шар поёдёт в сторону лузы, а биток пойдёт параллельно зелёной линии, касательной к прицельному шару (C) и воображаемому шару (M)
Система касательных прямых прицеливания битка использует прямую, проходящую через середину кия, для создания двух касательных прямых от битка в направлении прицельного шара. Две касательные прямые и прямая через середину битка пересекают прямую, проходящую через середину прицельного шара и центр лузы. Необходимо направить удар так, чтобы конечное положение битка (воображаемый шар на рисунке) касалось прицельного шара в точке касания прямой, перпендикулярной направлению на лузу (на рисунке эта касательная выделена зелёным цветом).
Длина окружности и площадь круга
Вот мы и подошли с вами к самому интересному, формулам длины окружности и площади круга, давайте их запишем:
Формулы длины окружности и площади круга
Эти формулы очень походы, в них есть двойка, число Pi и радиус, однако можно заметить, что у формулы длины окружности двойка слева, а у площади круга справа в степени.
Так как же их не путать? Очень просто: запомните, что вторая степень (или квадрат) должна быть у площади, значит двойка слева будет у длины.
Давайте это закрепим:
Задание на длину окружности и площадь круга в ЕГЭ и ОГЭ
Вот так просто и быстро мы закрепили сразу обе формулы.
Как находить площадь и длину дуги сектора круга: задачи
А теперь перейдём к самому интересному — нахождению площади и длины дуги сектора круга. Многие ученики думаю, что это сложно, но на самом деле это не так. Я предлагаю записать 2 коротких алгоритма, с помощью которых вы сможете легко найти площадь или длину дуги сектора.
2 алгоритма для поиска площади и длины дуги сектора
И конечно же давайте закрепим эти алгоритмы на практике:
Задача на поиск площади сектора круга в ЕГЭ и ОГЭ
Теперь вы умеете решать задания на поиск площади сектора. Согласитесь, что с алгоритмом всё намного понятнее и проще?
4 теоремы про окружность в ЕГЭ и ОГЭ
Теперь я предлагаю ознакомиться с теоремами, которые появляются в комбинациях различных прямых и отрезков в окружности.
Теорема № 1: теория и задания из ЕГЭ и ОГЭ
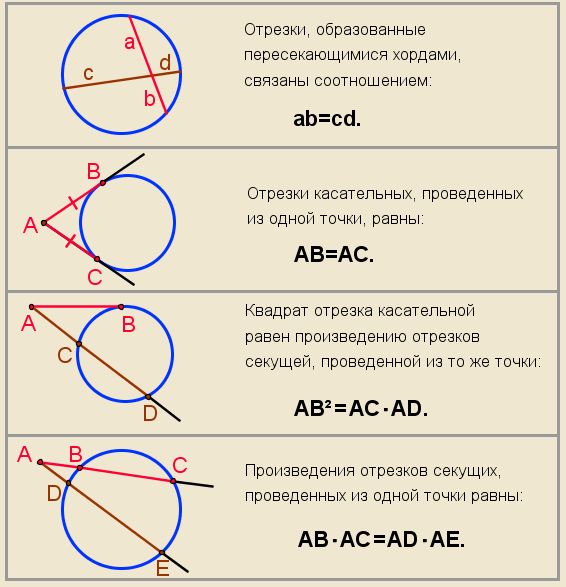
Первая теорема про хорду и касательную звучит так:
Угол между касательной и хордой равен половине дуге, которую стягивает хорда.
Подробнее с выведением вы можете ознакомиться на рисунке:
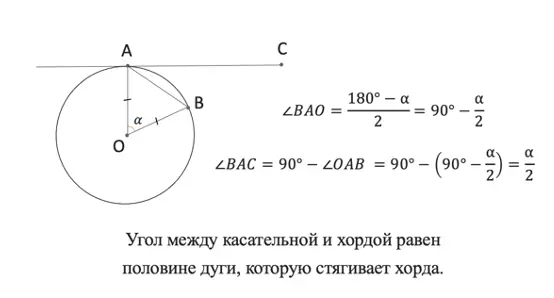Вот так выводится теорема про хорду и касательную
Однако хочу обратить ваше внимание, что если вы просто запомните формулировку, то многие задачи на окружность в ЕГЭ и ОГЭ покажутся вам супер-простыми и будут решаться в 1 действие. Давайте в этом убедимся:. Пример решения задачи на окружность в ЕГЭ и ОГЭ с использованием теоремы про хорду и касательную
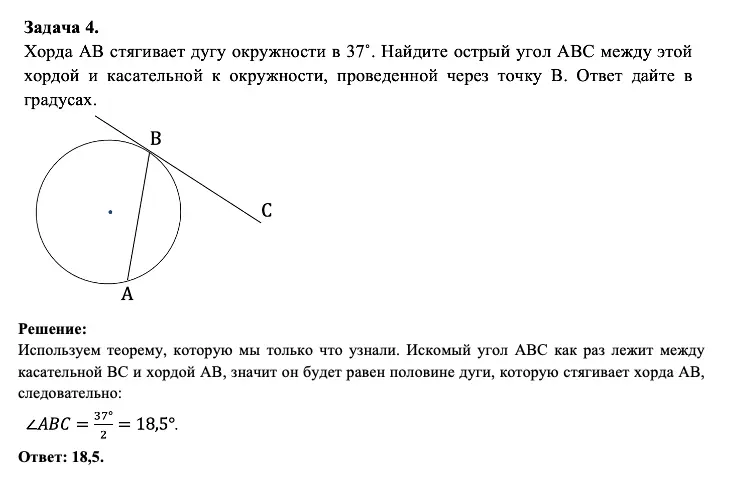Пример решения задачи на окружность в ЕГЭ и ОГЭ с использованием теоремы про хорду и касательную
Вот так просто и быстро в 1 действие мы справились с задачей. Правда здорово?!
Теорема № 2: теория и задания из ЕГЭ и ОГЭ
А теперь давайте посмотрим на одну из моих самых любимых теорем. А любимая она, потому что без неё некоторые задачи кажутся практически нерешаемыми, а с ней их можно решить быстро и просто! Звучит она так:
Квадрат касательной равен произведению секущей на её внешнюю часть. Я советую запоминать именно словесную формулировку, так как чертежи и буквы на них могут быть разными, и есть риск всё перепутать.
Наглядно познакомиться с теоремой можно на рисунке ниже:
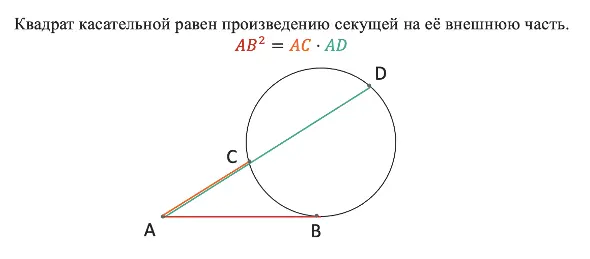Теорема: квадрат касательной равен произведению секущей на её внешнюю часть
И конечно же давайте отработаем на практике!
Пример задания на теорему № 2
Если бы мы не знали ту теорему, которую только что прошли, то было бы много версий, как можно решить задачу. Кто-то начал бы строить радиус к касательной и рассматривать треугольники, а кто-то просто не стал бы решать, однако у нас есть формула: давайте её используем!
Решение:
Вот так просто решается это задание!
Теорема № 3: теория и задания из ЕГЭ и ОГЭ
Если вы ещё не устали от теорем, то давайте познакомимся с ещё одной, которая связывает хорду с диаметром (радиусом).
Эта теорема интересна тем, что работает в обе стороны:
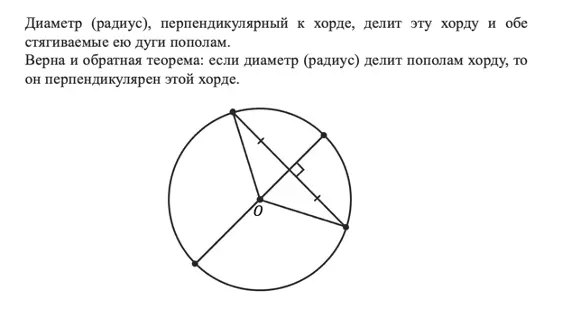Вот так хорду можно связать с диаметром (радиусом)
Конечно же я не могу оставить вас без тренировки, поэтому посмотрим на следующую задачу:
Задание на нашу теорему и его решение
Теорема № 4: пересекающиеся хорды
Последнее, с чем я вас познакомлю в контексте прямых и отрезков в окружности будет свойство пересекающихся хорд:
Произведения отрезков пересекающихся хорд равны.
Свойство пересекающихся хорд на рисунке
Для наглядности отрезки выделены разными цветами, так вам будет проще запомнить свойство.
А теперь отработаем его на практике:
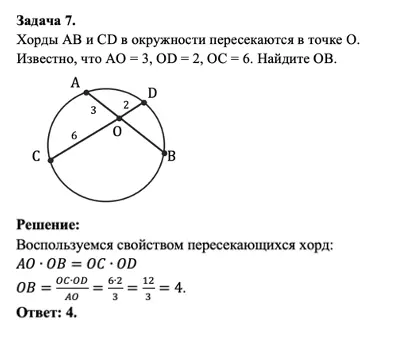Задание на свойство пересекающихся хорд и его решение
Алгоритм
В целях простоты алгоритма, будем считать, не теряя общности, что центр первой окружности имеет координаты . (Если это не так, то этого можно добиться простым сдвигом всей картины, а после нахождения решения — сдвигом полученных прямых обратно.)
![Math-public:ugly_v_okruzhnosti [президентский фмл №239]](https://uookn-kursk.ru/wp-content/uploads/d/7/c/d7cf5aaa1d9cc2a1c54c65cc1c335fb4.jpeg)
Обозначим через и радиусы первой и второй окружностей, а через — координаты центра второй окружности (точка отлична от начала координат, т.к. мы не рассматриваем случае, когда окружности совпадают, или одна окружность находится внутри другой).
Для решения задачи подойдём к ней чисто алгебраически. Нам требуется найти все прямые вида , которые лежат на расстоянии от начала координат, и на расстоянии от точки . Кроме того, наложим условие нормированности прямой: сумма квадратов коэффициентов и должна быть равна единице (это необходимо, иначе одной и той же прямой будет соответствовать бесконечно много представлений вида ). Итого получаем такую систему уравнений на искомые :
Чтобы избавиться от модулей, заметим, что всего есть четыре способа раскрыть модули в этой системе. Все эти способы можно рассмотреть общим случаем, если понимать раскрытие модуля как то, что коэффициент в правой части, возможно, умножается на .
Иными словами, мы переходим к такой системе:
Введя обозначения и , мы приходим к тому, что четыре раза должны решать систему:
Решение этой системы сводится к решению квадратного уравнения. Мы опустим все громоздкие выкладки, и сразу приведём готовый ответ:
Итого у нас получилось решений вместо . Однако легко понять, в каком месте возникают лишние решения: на самом деле, в последней системе достаточно брать только одно решение (например, первое). В самом деле, геометрический смысл того, что мы берём и , понятен: мы фактически перебираем, по какую сторону от каждой из окружностей будет прямая. Поэтому два способа, возникающие при решении последней системы, избыточны: достаточно выбрать одно из двух решений (только, конечно, во всех четырёх случаях надо выбрать одно и то же семейство решений).
Последнее, что мы ещё не рассмотрели — это как сдвигать прямые в том случае, когда первая окружность не находилась изначально в начале координат. Однако здесь всё просто: из линейности уравнения прямой следует, что от коэффициента надо отнять величину (где и — координаты первоначального центра первой окружности).
3.3.1 Сопряжение двух прямых дугой окружности
Все
задачи на сопряжение дугой могут быть
сведены к двум видам. Сопряжение
осуществляется либо заданным радиусом
сопрягающей дуги, либо через точку,
заданную на одной из сопрягаемых линий.
В том и другом случаях необходимо
построить центр сопрягающей дуги.
Сопряжение
двух пересекающихся прямых дугой
заданным радиусом R
c
(рисунок 49, а). Так как сопрягающая
дуга должна касаться заданных прямых,
то центр ее должен быть удален от каждой
прямой на величину равную радиусуR
c
.
Сопряжение строят так. Проводят две
прямые, параллельные заданным и удаленные
от них на величину радиусаR
c
и в пересечении этих прямых отмечают
точкуO
–
центр
сопрягающей дуги. Из точкиО
опускают перпендикуляр на каждую из
заданных прямых. Основания перпендикуляров
– точкиA
иB
–
являются
точками касания сопрягающей дуги. Такое
построение сопряжения справедливо для
двух пересекающихся прямых, составляющих
любой угол. Для сопряжения сторон прямого
угла можно воспользоваться также
способом, указанным на рисунке 49, б.
Рисунок
49
Сопряжение
двух пересекающихся прямых, на одной
из которых задана точка касания А
сопрягающей дуги
(рисунок 50).
Известно, что геометрическим местом
центров дуг, сопрягающих две пересекающиеся
прямые, является биссектриса угла,
образованного этими прямыми. Поэтому,
построив биссектрису угла, из точки
касанияA
восстанавливают
перпендикуляр к прямой до пересечения
его с биссектрисой и отмечают точку O
–
центр
сопрягающей дуги. Опустив из точки О
перпендикуляр на другую прямую, получают
вторую точку касания В и радиусом R
c
=
OA = OB
осуществляют сопряжение двух прямых,
на одной из которых была задана точка
касания.
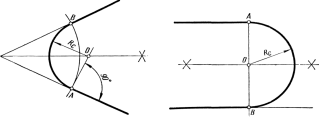
Сопряжение
двух параллельных прямых дугой, проходящей
через заданную точку касания А
(рисунок
51). Из точкиA
восставляют перпендикуляр к заданным
прямым и на пересечении его со второй
прямой отмечают точкуB
.
ОтрезокAB
делят
пополам и получают точкуО
–
центр сопрягающей дуги радиусом.
Рисунок
50 Рисунок 51
Реализация
Опишем сначала все необходимые структуры данных и другие вспомогательные определения:
struct pt {
double x, y;
pt operator- (pt p) {
pt res = { x-p.x, y-p.y };
return res;
}
};
struct circle pt {
double r;
};
struct line {
double a, b, c;
};
const double EPS = 1E-9;
double sqr (double a) {
return a * a;
}
Тогда само решение можно записать таким образом (где основная функция для вызова — вторая; а первая функция — вспомогательная):
void tangents (pt c, double r1, double r2, vector<line> & ans) {
double r = r2 - r1;
double z = sqr(c.x) + sqr(c.y);
double d = z - sqr(r);
if (d < -EPS) return;
d = sqrt (abs (d));
line l;
l.a = (c.x * r + c.y * d) z;
l.b = (c.y * r - c.x * d) z;
l.c = r1;
ans.push_back (l);
}
vector<line> tangents (circle a, circle b) {
vector<line> ans;
for (int i=-1; i<=1; i+=2)
for (int j=-1; j<=1; j+=2)
tangents (b-a, a.r*i, b.r*j, ans);
for (size_t i=; i<ans.size(); ++i)
ansi.c -= ansi.a * a.x + ansi.b * a.y;
return ans;
}
Касательные прямые к одной окружности
Касательная прямая t к окружности C пересекает окружность в единственной точке T. Для сравнения, секущие прямые пересекают окружность в двух точках, в то время как некоторые прямые могут не пересекать окружность совсем. Это свойство касательной прямой сохраняется при многих геометрических , таких как подобие, вращение, параллельный перенос, инверсия и картографическая проекция. Говоря техническим языком, эти преобразования не меняют структуру инцидентности касательных прямых и окружностей, даже если сами прямые и окружности деформируются.
Радиус окружности, проведённый через точку касания, перпендикулярен касательной прямой. И обратно, перпендикуляр к радиусу в конечной точке (на окружности) является касательной прямой. Окружность вместе с касательной прямой имеют осевую симметрию относительно радиуса (к точке касания).
По теореме о степени точки произведение длин PM•PN для любого луча PMN равно квадрату PT, длине отрезка от точки P до точки касания (отрезок показан красным цветом).
Никакая касательная прямая не может проходить через точку внутри окружности, поскольку любая такая прямая должна быть секущей. В то же время для любой точки, лежащей вне круга, можно построить две проходящие через неё касательные прямые. Геометрическая фигура, состоящая из окружности и двух касательных прямых, также обладает осевой симметрией относительно прямой, соединяющей точку P с центром окружности O (см. рисунок справа). В этом случае отрезки от точки P до двух точек касания имеют одинаковую длину. По теореме о степени точки квадрат длины отрезка до точки касания равен степени точки P относительно окружности C. Эта степень равна произведению расстояний от точки P до двух точек пересечения окружности любой секущей линией, проходящей через P.
Угол θ между хордой и касательной равен половине дуги, заключённой между концами хорды.
Касательная прямая t и точка касания T обладают свойством сопряжённости друг другу; это соответствие можно обобщить в идею о полюсе и поляре. Такая же взаимосвязь существует между точкой P вне окружности и секущей линией, соединяющей две точки касания.
Если точка P лежит вне окружности с центром O, и если касательные прямые из P касаются окружности в точках T и S, то углы ∠TPS и ∠TOS дают в сумме 180°.
Если хорда TM проведена из точки касания T прямой P T и ∠PTM ≤ 90°, то ∠PTM = (1/2)∠MOT.
Геометрическое построение
Построение касательной прямой к окружности (выделена красным) перпендикулярно радиусу.
Относительно легко построить прямую t, касательную к окружности в точке T на окружности. Для этого следует провести прямую a через центр окружности O и точку T. Тогда прямая t является перпендикуляром к прямой a. Один из способов построения перпендикуляра следующий (см. рисунок). Проводим тем же радиусом (r) окружность с центром в точке T, получаем вторую точку G на прямой a, а точка T становится серединой отрезка OG. Проводим две окружности радиуса R>r с центрами в точках O и G. Прямая, проходящая через точки пересечения этих окружностей, будет касательной.
Построение касательной прямой к окружности
Для построения касательной прямой через точку P к окружности C можно использовать свойство угла, опирающегося на диаметр окружности. Проводится окружность с центром в точке H, середине отрезка OP, где O — центр окружности C. Пересечения T и T‘ являются точками касания прямых, проходящих через точку P, поскольку углы ∠OTP и ∠OT‘P опираются на диаметр OP окружности с центром в H.
Теорема об описанном четырёхугольнике и вписанные окружности
Описанный четырёхугольник ABCD — это замкнутая фигура с четырьмя сторонами, которые касаются окружности C. Соответственно, C — вписанная в четырёхугольник ABCD окружность. По теореме Пито суммы противоположных сторон любого такого четырёхугольника равны, то есть
- AB¯+CD¯=BC¯+DA¯.{\displaystyle {\overline {AB}}+{\overline {CD}}={\overline {BC}}+{\overline {DA}}.}
Описанный четырёхугольник
Это заключение следует из равенства отрезков касательных от вершин четырёхугольника. Обозначим точки касания как P (на отрезке AB), Q (на отрезке BC), R (на отрезке CD) и S (на отрезке DA). Симметричные отрезки до точек касания от каждой вершины четырёхугольника ABCD равны, то есть BP=BQ=b, CQ=CR=c, DR=DS=d и AS=AP=a.
Но каждая сторона четырёхугольника состоит из двух таких отрезков
- AB¯+CD¯=(a+b)+(c+d)=BC¯+DA¯=(b+c)+(d+a){\displaystyle {\overline {AB}}+{\overline {CD}}=(a+b)+(c+d)={\overline {BC}}+{\overline {DA}}=(b+c)+(d+a)},
что и доказывает утверждение.
Обратное утверждение также верно — окружность можно вписать в любой выпуклый четырёхугольник, у которого суммы длин противоположных сторон равны.
Зависимость между углами, дугами и хордами
Теорема 57. В двух равных кругах равным углам при центре соответствуют равные дуги.
Дано. Две окружности описаны (черт. 88) одними и теми же радиусами и углы при центре равны:
∠AOB = ∠A’O’B’.
Требуется доказать, что ◡AB = ◡A’B’.
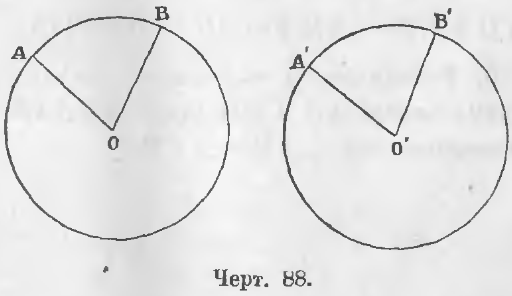
Доказательство. Наложим круг O’ на круг O так, чтобы центр O’ совпал с центром O и сторона OA со стороною O’A’. Точка A’ по равенству радиусов совпадает с точкой A. По равенству углов A’O’B’ и AOB отрезок O’B’ пойдет по отрезку OB и по равенству радиусов точка B’ упадет в точку B. Две крайние точки дуги A’B’ совпадут с двумя крайними точками дуги AB, следовательно, и все промежуточные точки дуги A’B’ совпадут с промежуточными точками дуги AB, так как окружность O’ совпадает с окружностью O, ибо они описаны равными радиусами.
Теорема 58 (обратная 57). Равным дугам соответствуют равные углы.
Дано. Дуги AB и A’B’ равны (◡AB = ◡A’B’) (черт. 88).
Требуется доказать, что ∠AOB = ∠A’O’B’.
Доказательство. Наложим сектор A’O’B’ на сектор AOB так, чтобы отрезок O’A’ совпал с отрезком OA. Дуга A’B’ упадет на дугу AB и B’ упадет в B. Отрезок B’O’ совпадет с отрезком BO и угол AOB совпадет с углом A’O’B’, следовательно,
∠AOB = ∠A’O’B’ (ЧТД).
Теорема 59. Диаметр больше всякой хорды.
Даны диаметр CD и хорда MN (черт. 87).
Требуется доказать, что CD > MN.
Доказательство. Проведем радиусы MO и NO. Ломаная линия MON больше прямой MN
MON > MN или MO + ON > MN
Так как MO = CO, NO = OD, то заменяя MO и NO равными им величинами, получим неравенства:
CO + OD > MN или CD > MN (ЧТД).
Теорема 60. Равные хорды стягивают равные дуги.
Даны равные хорды AB и CD (черт. 89) (AB = CD).
Требуется доказать, что ◡AB = ◡CD.
Доказательство. Соединив точки A, B, C, D с центром, имеем
∆AOB = ∆COD, ибо
OA = OC и OB = OD как радиусы, AB = CD по условию.
Следовательно, ∠AOB = ∠COD, откуда ◡AB = ◡CD (ЧТД).
Теорема 61 (обратная 60). Равные дуги стягиваются равными хордами.
Дано. Дуги AB и CD равны (черт. 89) (◡AB = ◡CD).
Требуется доказать, что AB = CD.
Доказательство. Два треугольника AOB и COD равны, ибо OA = OC и OB = OD как радиусы, ∠AOB = ∠COD ибо по условию дуги AB и CD равны, а потому и углы равны (теорема 58). Следовательно, AB = CD (ЧТД).
Теорема 62. Если дуги меньше полуокружности, то против большей дуги лежит большая хорда.
Дано. Дуга BD больше дуги AC (черт. 90) (◡BD > ◡AC).
Требуется доказать, что BD > AC.
Доказательство. Соединим точки A, C, B, D с центром O. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BOD > AOC. Следовательно, BD > AC (теорема 23) (ЧТД).
Теорема 63 (обратная 62). Против большей хорды лежит большая дуга.
Дано. Хорда BD больше хорды AC (черт. 90) (BD > AC).
Требуется доказать, что ◡BD > ◡AC.
Доказательство. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BD > AC по условию. Поэтому ∠BOD > ∠AOC (теорема 24). Следовательно, ◡BD > ◡AC (ЧТД).
Измерение углов
Центральные углы. Углы, имеющие вершину при центре, называются центральными углами.
Относительно этих углов имеют место следующие теоремы.
Теорема 74. Равным центральным углам в одной и той же окружности соответствуют равные дуги.
Дано. Углы AOB и COD равны (черт. 109).
Требуется доказать, что ◡AB = ◡CD.
Доказательство. Проведем хорды AB и CD и соединим точки A, B, C, D с центром. Два треугольника AOB и COD равны, ибо AO = CO и BO = DO как радиусы, ∠AOB = ∠COD по условию. Следовательно, хорды AB и CD равны.
Против равных хорд лежат равные дуги, следовательно и дуги AB и CD равны: ◡AB = ◡CD (ЧТД).
Теорема 75 (обратная 74). Равным дугам в одной и той же окружности соответствуют равные углы.
Дано. Дуги AB и CD равны (черт. 109).
Требуется доказать, что ∠AOB = ∠COD.
Доказательство. Из того, что дуги AB и CD равны, следует, что и хорды AB и CD тоже равны (теорема 61).
Два треугольника AOB и COD равны, ибо AB = CD как равные хорды, AO = CO и BO = DO как радиусы. Следовательно, ∠AOB = ∠COD (ЧТД).
Теорема 76. Отношение центральных углов равно отношению соответствующих им дуг.
Даны два центральные угла AOB и COD (черт. 110).
Требуется доказать, что
AOB/COD = AB/CD.
Доказательство. Здесь имеют место два случая:
1) Когда дуги AB и CD соизмеримы и 2) когда они несоизмеримы.
1-й случай. Дуги AB и CD соизмеримы.
Пусть дуга AE будет их общей мерой. Положим, что она p раз содержится в дуге AB и q раз в дуге CD. Разделив дугу AB на p, а CD на q равных частей и соединив точки деления дуг с центром O, мы разделим угол AOB на p, а угол COD на q равных углов, из которых каждый равен углу AOE.
Из равенств
AB = pAE, CD = qAE
AOB = pAOE, COD = qAOE
получаем
AOB/COD = p/q, AB/CD = p/q, откуда
AOB/COD = AB/CD (ЧТД).
2-й случай. Дуги AB и CD несоизмеримы.
Отложим дугу AF равную CD и соединим F с O. Углы AOF и COD равны.
Требуется доказать, что
AOB/AOF = AB/AF
Доказательство. A) Положим
AOB/AOF > AB/AF (1).
Для того, чтобы имело место равенство, нужно дробь во второй части неравенства (1) увеличить. Для этого следует ее знаменатель уменьшить.
Положим, мы нашли, что имеет место равенство
AOB/AOF = AB/AG (a)
Разделим дугу AB на равное число таких частей, чтобы каждая часть была менее GF; тогда одна из точек деления i упадет в промежутке между G и F. Дуги AB и Ai соизмеримы, следовательно,
AOB/AOi = AB/Ai (b).
Разделив равенства (b) на (a), находим
AOF/AOi = AG/Ai
равенство несообразное, ибо первая часть его больше, а вторая меньше 1, следовательно, допущение (1) не имеет места.
B) Допустим, что
AOB/AOF < AB/AF (2)
Тогда вторую часть этого неравенства нужно уменьшить для того, чтобы имело место равенство. Для этого нужно знаменатель дроби AB/AF увеличить. Положим, мы нашли такую точку H, чтобы удовлетворялось равенство
AOB/AOF = AB/AH (c)
Разделив дугу AB на такие равные части, чтобы каждая часть была меньше FH, мы найдем, что одна из точек деления J упадет в промежуток между F и H. Дуги AB и AJ будут соизмеримы, следовательно,
AOB/AOJ = AB/AJ (d)
Разделив равенство (d) на (c) найдем
AOF/AOJ = AH/AJ
Это равенство несообразно, ибо первое отношение меньше, а второе больше единицы, следовательно, и допущение (2) тоже не имеет места, откуда видно, что справедливо только равенство AOB/AOF = AB/AF (ЧТД).
Зная, что отношение углов равно отношению дуг, описанных равными радиусами, мы в пропорции (черт. 111)
AOB/COD = AB/CD
можем принять за единицу любую дугу. В этом случае должны принять за единицу и соответствующий ей угол.
Принимая дугу CD, а следовательно, и угол COD за 1, имеем равенство
AOB/1 = AB/1
или отношение угла к своей единице равно отношению дуги к своей соответствующей единице, откуда
∠AOB = ◡AB.
Это равенство означает, что
числовая величина угла равна числовой величине дуги, или что угол измеряется дугой, описанной из его вершины, как из центра.
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |
 |
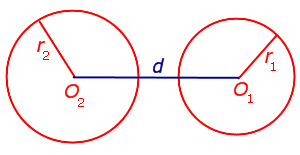Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2определяется расстоянием d между центрами этих окружностей
Каждая из окружностей лежит вне другой
Расстояние между центрами окружностей больше суммы их радиусов
Внешнее касание двух окружностей
Расстояние между центрами окружностей равно сумме их радиусов
Внутреннее касание двух окружностей
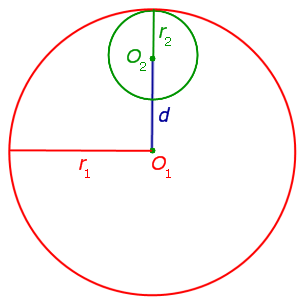
Расстояние между центрами окружностей равно разности их радиусов
Окружности пересекаются в двух точках
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1– r2 лежит внутри другой
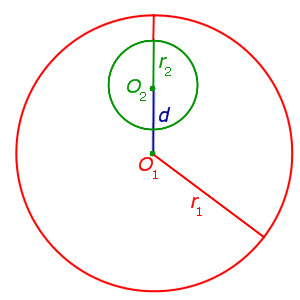
Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2определяется расстоянием d между центрами этих окружностей
Каждая из окружностей лежит вне другой
Расстояние между центрами окружностей больше суммы их радиусов
Внешнее касание двух окружностей
Расстояние между центрами окружностей равно сумме их радиусов
Внутреннее касание двух окружностей
Расстояние между центрами окружностей равно разности их радиусов
Окружности пересекаются в двух точках
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1– r2 лежит внутри другой
Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2определяется расстоянием d между центрами этих окружностей
Каждая из окружностей лежит вне другой
Расстояние между центрами окружностей больше суммы их радиусов
Внешнее касание двух окружностей
Расстояние между центрами окружностей равно сумме их радиусов
Внутреннее касание двух окружностей
Расстояние между центрами окружностей равно разности их радиусов
Окружности пересекаются в двух точках
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1– r2 лежит внутри другой
Расстояние между центрами окружностей меньше разности их радиусов
d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Внутренняя касательная к двум окружностям
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Внутреннее касание двух окружностей
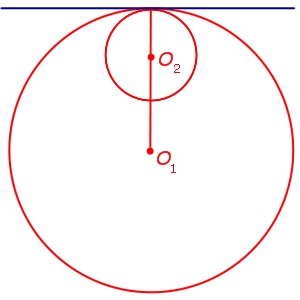
Существует единственная общая внешняя касательная. Других общих касательных нет.
Окружности пересекаются в двух точках
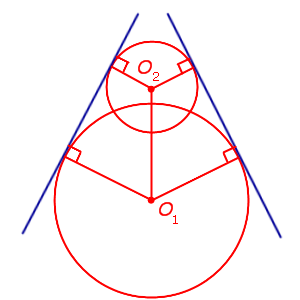
Существуют две общих внешних касательных. Других общих касательных нет.
Внешнее касание двух окружностей
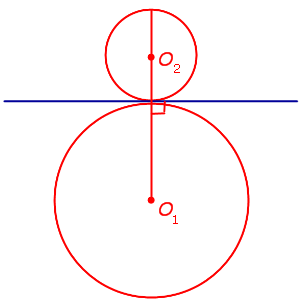
Существует единственная общая внутренняя касательная, а такжедве общих внешних касательных. Других общих касательных нет.
Каждая из окружностей лежит вне другой
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
| Внешняя касательная к двум окружностям |
 |
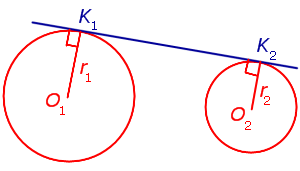Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Внутренняя касательная к двум окружностям
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Внутреннее касание двух окружностей
Существует единственная общая внешняя касательная. Других общих касательных нет.
Окружности пересекаются в двух точках
Существуют две общих внешних касательных. Других общих касательных нет.
Внешнее касание двух окружностей
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.
Каждая из окружностей лежит вне другой
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
Интересный факт
Построение касательной.
Построение касательных – одна из тех задач, которые привели к рождению дифференциального исчисления. Первый опубликованный труд, относящийся к дифференциальному исчислению и принадлежащий перу Лейбница, имел название «Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления».
Геометрические познания древних египтян.
Если не учитывать весьма скромный вклад древних обитателей долины между Тигром и Евфратом и Малой Азии, то геометрия зародилась в Древнем Египте до 1700 до н.э. Во время сезона тропических дождей Нил пополнял свои запасы воды и разливался. Вода покрывала участки обработанной земли, и в целях налогообложения нужно было установить, сколько земли потеряно. Землемеры использовали в качестве измерительного инструмента туго натянутую веревку. Еще одним стимулом накопления геометрических знаний египтянами стали такие виды их деятельности, как возведение пирамид и изобразительное искусство.
Об уровне геометрических познаний можно судить из древних рукописей, которые специально посвящены математике и являются чем-то вроде учебников, или, вернее, задачников, где даны решения разных практических задач.
Древнейшая математическая рукопись египтян переписана неким учеником между 1800 – 1600 г.г. до н.э. с более древнего текста. Папирус разыскал русский египтолог Владимир Семенович Голенищев. Он хранится в Москве — в Музее изобразительных искусств имени А.С. Пушкина, и называется Московским папирусом.
Другой математический папирус, написанный лет на двести-триста позднее Московского, хранится в Лондоне. Он называется: „Наставление, как достигнуть знания всех тёмных вещей, всех тайн, которые скрывают в себе вещи… По старым памятникам писец Ахмес написал это». Рукопись так и называют „папирусом Ахмеса», или папирусом Райнда — по имени англичанина, который разыскал и купил этот папирус в Египте. В папирусе Ахмеса даётся решение 84 задач на различные вычисления, которые могут понадобиться на практике.
