Простейшие и сложные тригонометрические неравенства

Общий способ сравнения чисел

Число а больше числа b (а>b), если их разность (а — b) — положительное число; число а меньше числа b, если их разность (а — b) — отрицательное число.

Свойства числовых неравенств:

1. Если a>b, то b<а; если a<b, то b>a;
2. Если a<b и b<c, то a<b<c;
3. Если a<b и $c\in\mathbb{R}$, то a+c<b+c;
4. Если а<b и с>0, то ас<bс; если а<b и с<0, то ac>bc;
5. Если a<b и c<d, то a+c<b+d;
6. Если a<b и c<d и а, b, с, d — положительные числа, то ac<bd.

Решение неравенства с одной переменной — это значение переменной, при котором неравенство обращается в верное числовое неравенство.

Решить неравенство с одной переменной означает найти все его решения или доказать, что решений нет.

Решение системы неравенств с одной переменной — это значение переменной, при котором верно каждое из неравенств системы.

Решить систему означает найти все ее решения или доказать, что решений нет.

Не равно, больше, меньше

Иногда ценность представляет именно сам факт неравенства двух объектов. А когда сравниваются значения каких-либо величин, то, выяснив их неравенство, обычно идут дальше, и выясняют, какая величина больше, а какая – меньше.

Смысл слов «больше» и «меньше» мы познаем практически с первых дней нашей жизни. На интуитивном уровне мы воспринимаем понятие больше и меньше в плане размера, количества и т.п. А дальше постепенно начинаем осознавать, что при этом фактически речь идет о сравнении чисел, отвечающим количеству некоторых предметов или значениям некоторых величин. То есть, в этих случаях мы выясняем, какое из чисел больше, а какое – меньше.

Приведем пример. Рассмотрим два отрезка AB и CD, и сравним их длины . Очевидно, они не равны, также очевидно, что отрезок AB длиннее отрезка CD. Таким образом, согласно смыслу слова «длиннее», длина отрезка AB больше длины отрезка CD, и в то же время длина отрезка CD меньше длины отрезка AB.

Еще пример. С утра была зафиксирована температура воздуха 11 градусов Цельсия, а в обед – 24 градуса. Согласно правилам сравнения натуральных чисел, 11 меньше 24, следовательно, значение температуры с утра было меньше, чем ее значение в обед (температура в обед стала больше, чем была температура с утра).

Свойства неравенств

Согласно тому, как мы ввели понятие неравенства, можно описать основные свойства неравенств. Понятно, что объект не может быть не равен самому себе. В этом состоит первое свойство неравенств. Второе свойство не менее очевидно: если первый объект не равен второму, то второй не равен первому.

Введенные на некотором множестве понятия «меньше» и «больше» задают на исходном множестве так называемые отношения «меньше» и «больше». Это же относится и к отношениям «меньше или равно» и «больше или равно». Они также обладают характерными свойствами.

Начнем со свойств отношений, которым соответствуют знаки < и >. Перечислим их, после чего дадим необходимые комментарии для пояснения:

• антирефлексивность;
• антисимметричность;
• транзитивность.

Свойство антирефлексивности с помощью букв можно записать так: для любого объекта a неравенства a>a и a<a – являются неверными. Свойство антисимметричности утверждает, что если первый объект больше (меньше) второго, то второй объект соответственно меньше (больше) первого. В формальной записи, если a>b, то b<a, а также, если a<b, то b>a. Наконец, свойство транзитивности состоит в том, что из a<b и b<c следует, что a<c, а также, из a>b и b>c следует, что a>c. Это свойство также воспринимается достаточно естественно: если первый объект меньше (больше) второго, а второй меньше (больше) третьего, то понятно, что первый объект подавно меньше (больше) третьего.

В свою очередь отношениям «меньше или равно» и «больше или равно» присущи следующие свойства:

• рефлексивности: имеют место неравенства a≤a и a≥a (так как они включают в себя случай a=a);
• антисимметричности: если a≤b, то b≥a, и если a≥b, то b≤a;
• транзитивности: из a≤b и b≤c следует, что a≤c, а из a≥b и b≥c следует, что a≥c.

Примеры решения разных видов неравенств

Для того чтобы добавить наглядности в теорию про решение неравенств, ниже приведены примеры.

Первый пример. 2х — 4 > 1 + х

Решение: для того чтобы определить ОДЗ, достаточно просто внимательно посмотреть на неравенство. Оно образовано из линейных функций, поэтому определено при всех значениях переменной.

Теперь из обеих частей неравенства нужно вычесть (1 + х). Получается: 2х — 4 — (1 + х) > 0. После того как будут раскрыты скобки и приведены подобные слагаемые неравенство примет такой вид: х — 5 > 0.

Приравняв его к нулю, легко найти его решение: х = 5.

Теперь эту точку с цифрой 5, нужно отметить на координатном луче. Потом проверить знаки исходной функции. На первом интервале от минус бесконечности до 5 можно взять число 0 и подставить его в неравенство, получившееся после преобразований. После расчетов получается -7 >0. под дугой интервала нужно подписать знак минуса.

На следующем интервале от 5 до бесконечности можно выбрать число 6. Тогда получается, что 1 > 0. Под дугой подписан знак «+». Этот второй интервал и будет ответом неравенства.

Ответ: х лежит в интервале (5; ∞).

Второй пример. Требуется решить систему двух уравнений: 3х + 3 ≤ 2х + 1 и 3х — 2 ≤ 4х + 2.

Решение. ОДЗ этих неравенств тоже лежит в области любых чисел, поскольку даны линейные функции.

Дальше действовать нужно поэтапно. Сначала преобразовать первое из неравенств и приравнять его к нулю. 3х + 3 — 2х — 1 = 0. То есть х + 2 = 0. Таким образом, х равен -2.

Второе неравенство примет вид такого уравнения: 3х — 2 — 4х — 2 = 0. После преобразования: -х — 4 =0. Из него получается значение для переменной, равное -4.

Эти два числа нужно отметить на оси, изобразив интервалы. Поскольку неравенство нестрогое, то все точки нужно закрасить. Первый интервал от минус бесконечности до -4. Пусть будет выбрано число -5. Первое неравенство даст значение -3, а второе 1. Значит, этот промежуток не входит в ответ.

Второй интервал от -4 до -2. Можно выбрать число -3 и подставить его в оба неравенства. В первом и во втором получается значение -1. Значит, под дугой «-».

На последнем интервале от -2 до бесконечности самым лучшим числом является ноль. Его и нужно подставить и найти значения неравенств. В первом из них получается положительное число, а втором ноль. Этот промежуток тоже нужно исключить из ответа.

Из трех интервалов решением неравенства является только один.

Ответ: х принадлежит .

Третий пример. |1 — х| > 2 |х — 1|.

Решение. Первым делом нужно определить точки, в которых функции обращаются в ноль. Для левого этим числом будет 2, для правого — 1. их нужно отметить на луче и определить промежутки знакопостоянства.

На первом интервале, от минус бесконечности до 1, функция из левой части неравенства принимает положительные значения, а из правой — отрицательные. Под дугой нужно записать рядом два знака «+» и «-».

Следующий промежуток от 1 до 2. На нем обе функции принимают положительные значения. Значит, под дугой два плюса.

Третий интервал от 2 до бесконечности даст такой результат: левая функция — отрицательная, правая — положительная.

С учетом получившихся знаков нужно вычислить значения неравенства для всех промежутков.

На первом получается такое неравенство: 2 — х > — 2 (х — 1). Минус перед двойкой во втором неравенстве получился из-за того, что эта функция отрицательная.

После преобразования неравенство выглядит так: х > 0. Оно сразу дает значения переменной. То есть из этого интервала в ответ пойдет только промежуток от 0 до 1.

На втором: 2 — х > 2 (х — 1). Преобразования дадут такое неравенство: -3х + 4 больше ноля. Его нулем будет значение х = 4/3. С учетом знака неравенства получается, что х должен быть меньше этого числа. Значит, этот интервал уменьшается до промежутка от 1 до 4/3.

Последний дает такую запись неравенства: — (2 — х) > 2 (х — 1). Его преобразование приводит к такому: -х > 0. То есть уравнение верно при х меньшем ноля. Это значит, что на искомом промежутке неравенство не дает решений.

На первых двух промежутках граничным оказалось число 1. Его нужно проверить отдельно. То есть подставить в исходное неравенство. Получается: |2 — 1| > 2 |1 — 1|. Подсчет дает что 1 больше 0. Это верное утверждение, поэтому единица входит в ответ.

Ответ: х лежит в промежутке (0; 4/3).

Графический способ

Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.

Алгоритм решения y = ax + b графическим способом

• во время решения ax + b < 0 определить промежуток, где график изображен ниже оси Ох;
• во время решения ax + b ≤ 0 определить промежуток, где график изображается ниже Ох или совпадает с осью;
• во время решения ax + b > 0 определить промежуток, где график изображается выше Ох;
• во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.

Рассмотрим пример: −5 * x − √3 > 0.

Как решаем

Так как коэффициент при x отрицательный, данная прямая является убывающей.
Координаты точки пересечения с Ох равны (−√3 : 5; 0).
Неравенство имеет знак >, значит нужно обратить внимание на промежуток выше оси Ох.
Поэтому открытый числовой луч (−∞, −√3 : 5) будет решением.

Ответ: (−∞, −√3 : 5) или x < −√3 : 5.

Линейные неравенства в 8 классе — это маленький кирпич, который будет заложен в целый фундамент знаний. Мы верим, что у все получится!

Тождественные преобразования неравенств.

Тождественные преобразования неравенств очень похожи на Собственно, в этом и есть основная проблема. Отличия проскакивают мимо головы и… приехали.) Поэтому я особо выделю эти отличия. Итак, первое тождественное преобразование неравенств:

1. К обеим частям неравенства можно прибавить (отнять) одно и то же число, или выражение. Любое. Знак неравенства от этого не изменится.

На практике это правило применяется как перенос членов из левой части неравенства в правую (и наоборот) со сменой знака. Со сменой знака члена, а не неравенства! Правило один в один совпадает с правилом для уравнений. А вот следующие тождественные преобразования в неравенствах существенно отличается от таковых в уравнениях. Поэтому я выделяю их красным цветом:

2. Обе части неравенства можно умножить (разделить) на одно и то же положительное число. На любое положительное число. Знак неравенства от этого не изменится.

3. Обе части неравенства можно умножить (разделить) на одно и то же отрицательное число. На любое отрицательное число. Знак неравенства от этого изменится на противоположный.

Вы помните (надеюсь…), что уравнение можно умножать/делить на что попало. И на любое число, и на выражение с иксом. Лишь бы не на ноль. Ему, уравнению, от этого ни жарко, ни холодно.) Не меняется оно. А вот неравенства более чувствительны к умножению/делению.

Наглядный пример на долгую память. Напишем неравенство, не вызывающее сомнений:

5 > 2

Умножим обе части на +3, получим:

15 > 6

Возражения есть? Возражений нет.) А если умножим обе части исходного неравенства на -3, получим:

-15 > -6

А это уже откровенная ложь.) Полное враньё! Обман народа! Но стоит изменить знак неравенства на противоположный, как всё становится на свои места:

-15 < -6

Про враньё и обман — это я не просто так ругаюсь.) «Забыл сменить знак неравенства…» — это главная ошибка в решении неравенств. Это пустяковое и несложное правило стольких людей ушибло! Которые забыли…) Вот и ругаюсь. Может, запомнится…)

Особо внимательные заметят, что неравенство нельзя умножать на выражение с иксом. Респект внимательным!) А почему нельзя? Ответ простой. Мы же не знаем знак этого выражения с иксом. Оно может быть положительное, отрицательное… Стало быть, мы не знаем, какой знак неравенства ставить после умножения. Менять его, или нет? Неизвестно. Разумеется, это ограничение (запрет умножения/деления неравенства на выражение с иксом) можно обойти. Если очень надо будет. Но это тема для других уроков.

Вот и все тождественные преобразования неравенств. Ещё раз напомню, что они работают для любых неравенств. А теперь можно переходить к конкретным видам.

Запись неравенств с помощью знаков

Существуют общепринятые обозначения для записи неравенств:

•  знак «не равно», представляющий собой перечеркнутый знак «равно»: ≠. Этот знак располагается между неравными объектами. Например: 5≠10 пять не равно десяти;
•  знак «больше»: > и знак «меньше»: <. Первый записывается между большим и меньшим объектами; второй между меньшим и большим. Например, запись о сравнении отрезков вида |AB| > |CD| говорит о том, что отрезок AB больше отрезка СD;
• знак «больше или равно»: ≥ и знак «меньше или равно»: ≤.

Подробнее их смысл разберем ниже. Дадим определение неравенств по виду их записи.

Строгие и нестрогие неравенства

1. Знаки строгих неравенств – это знаки «больше» и «меньше»: > и < Неравенства, составленные с их помощью – строгие неравенства.
2. Знаки нестрогих неравенств – это знаки «больше или равно» и «меньше или равно»: ≥ и ≤. Неравенства, составленные с их помощью – нестрогие неравенства.

Как применяются строгие неравенства, мы разобрали выше. Зачем же используются нестрогие неравенства? В практике такими неравенствами возможно задавать случаи, описываемые словами «не больше» и «не меньше». Фраза «не больше» означает меньше или столько же – этому уровню сравнения соответствует знак «меньше или равно» ≤. В свою очередь, «не меньше» значит – столько же или больше, а это знак «больше или равно» ≥. Таким образом, нестрогие неравенства, в отличие от строгих, дают возможность равенства объектов.

Верные и неверные неравенства

Приведем простые примеры для наглядности:

Пример 2

Неравенство 5≠5 является неверным, поскольку на самом деле числа 5 и 5 равны.

Или такое сравнение:

Пример 3

Допустим S – площадь некой фигуры, в этом случае S<-4 является верным неравенством, поскольку площадь всегда выражена неотрицательным числом.

Аналогичными по смыслу термину «верное неравенство» являются фразы «справедливое неравенство», «имеет место неравенство» и т.д.

Двойные, тройные и т.п. неравенства

Свойство транзитивности дает возможность записывать двойные, тройные и так далее неравенства, по сути являющиеся цепочками неравенств. К примеру: двойное неравенство –  e >f>g или тройное неравенство k1≤ k2≤ k3 ≤k4.

Отметим, что удобным бывает записывать неравенство как цепочки, включающие в себя различные знаки: равно, не равно и знаки строгих и нестрогих неравенств. Например, x=2<>

Как быть с дробными неравенствами?

Поскольку во время их решения может потребоваться изменение знака неравенства, то нужно очень тщательно и внимательно выполнять все пункты плана. Иначе может получиться противоположный ответ.

Решение дробных неравенств тоже использует метод интервалов. И план действий будет таким:

• Используя описанные свойства, придать дроби такой вид, чтобы справа от знака остался только ноль.
• Заменить неравенство на «=» и определить точки, в которых функция будет равна нулю.
• Отметить их на координатной оси. При этом числа, получившиеся в результате расчетов в знаменателе, всегда будут выколоты. Все другие — исходя из условия неравенства.
• Определить интервалы знакопостоянства.
• В ответ записать объединение тех промежутков, знак которых соответствует тому, который был в исходном неравенстве.

Строгие и нестрогие неравенства

Определение.

Знаки меньше называют знаками строгих неравенств, а записанные с их помощью неравенства – строгими неравенствами.

В свою очередь

Определение.

Знаки меньше или равно ≤ и больше или равно ≥ называют знаками нестрогих неравенств, а составленные с их использованием неравенства – нестрогими неравенствами.

Сфера применения строгих неравенств понятна из вышеприведенной информации. А для чего нужны нестрогие неравенства? На практике с их помощью удобно моделировать ситуации, которые можно описать фразами «не больше» и «не меньше». Фраза «не больше» по сути означает меньше или столько же, ей отвечает знак меньше или равно вида ≤. Аналогично, «не меньше» значит столько же или больше, ей соответствует знак больше или равно ≥.

Отсюда становится понятно, почему знаки < и > получили название знаков строгих неравенств, а ≤ и ≥ — нестрогих. Первые исключают возможность равенства объектов, а вторые – допускают ее.

В заключение этого пункта покажем пару примеров использования нестрогих неравенств. Например, с помощью знака больше или равно можно записать тот факт, что модуль числа a является неотрицательным числом, как |a|≥0. Еще пример: известно, что среднее геометрическое двух положительных чисел a и b меньше или равно их среднему арифметическому, то есть, .

Проверьте себя.

Какое из этих неравенств можно было бы решать методом отбрасывания общего знаменателя и почему?

\
\

Приводим дроби к общему знаменателю. Дополнительные множители в первом неравенстве 8 и 3, во втором — 7 и \((x-1)\).
\
Уже видно, где есть множитель, содержащий неизвестную величину, но пока ничего не нарушено, т.к. при приведении к общему знаменателю и числитель, и знаменатель дроби мы умножаем на одно и то же число (выражение). От этого действия её значение не изменяется.
\
Отбрасывание знаменателя в первом неравенстве равносильно умножению обеих его частей на положительное число 24, что по свойству 4 сохраняет неравенство верным.
\
Для второго неравенства аналогичное действие привело бы к умножению на двучлен с неизвестным знаком \(7x-7\). А если не вспомнить о свойствах неравенств, то к ошибочному решению \(21 > 8x-8.\)

Выход из положения может быть следующим:

Если \(7x-7 > 0\), то знак исходного неравенства сохраняется:
\
Если \(7x-7 \frac{8x-8}{7x-7} \Leftrightarrow 21 \frac{8x-8}{7x-7} \Leftrightarrow
\left[ {\begin{array}{*{20}c}
{\left\{ {\begin{array}{*{20}c}
{7x-7>0;} \\
{21 > 8x-8} \hfill \\
\end{array} } \right.} \\
{\left\{ {\begin{array}{*{20}c}
{7x -7Вывод: Отбрасывание общего знаменателя можно производить только для тех неравенств, в которых этот знаменатель положительная константа. Т.е. здесь для неравенства (1). Во всех остальных случаях требуется более детальный анализ знаков чисел и выражений.

Показать ответ.

Пять видов неравенств и способы их решений

Первый вид неравенств

Естественно, знак неравенства может быть и нестрогим.

Здесь и далее большими буквами \( A\), \( B\), \( C\) и т.д. я буду обозначать не переменные или параметры, а целые выражения, содержащие переменную.

Так, общая запись \( \sqrt{A}>\sqrt{B}\) соответствует, например, уравнению \( \sqrt{{{x}^{2}}-{x}-2}>\sqrt{{x}-1}\).

Здесь \( A={{x}^{2}}-{x}-2\) и \( B={x}-1\).

Как решить такое неравенство?

Для начала вспомним, что функция \( f\left( x \right)=\sqrt{x}\) – монотонна, то есть, чем больше подкоренное выражение, тем больше сам корень.

Поэтому из двух корней больше тот, у которого подкоренное выражение больше.

Но недаром мы недавно вспоминали про ОДЗ. Есть ли какие-нибудь ограничения в этом неравенстве?

Действительно, чтобы неравенство имело смысл, необходимо, чтобы оба подкоренных выражения были неотрицательны:

\( \left\{ \begin{array}{l}A\ge 0\\B\ge 0\end{array} \right.\)Но поскольку первое выражение больше второго, достаточно потребовать неотрицательности только второго:

или

Простейшие тригонометрические неравенства

Примером простейшего тригонометрического неравенства является: sin x ‹  1/2. Решать подобные задачи принято графически, для этого разработаны два способа.

Способ 1 — Решение неравенств с помощью построения графика функции

Чтобы найти промежуток, удовлетворяющий условиям неравенство sin x ‹ 1/2, необходимо выполнить следующие действия:

1. На координатной оси построить синусоиду y = sin x.
2. На той же оси начертить график числового аргумента неравенства, т. е. прямую, проходящую через точку ½ ординаты ОY.
3. Отметить точки пересечения двух графиков.
4. Заштриховать отрезок являющийся, решением примера.

Когда в выражении присутствуют строгие знаки, точки пересечения не являются решениями. Так как наименьший положительный период синусоиды равен 2π, то запишем ответ следующим образом:

Если знаки выражения нестрогие, то интервал решений необходимо заключить в квадратные скобки — . Ответ задачи можно также записать в виде очередного неравенства: 

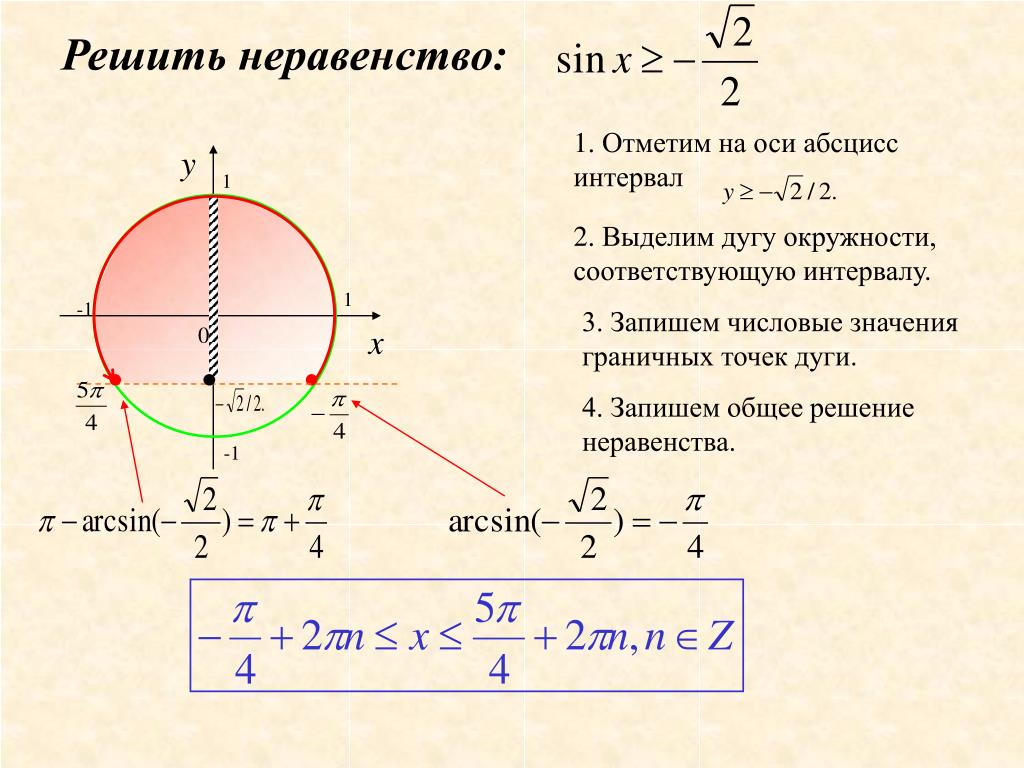
Способ 2 — Решение тригонометрических неравенств с помощью единичной окружности

Подобные задачи легко решаются и с помощью тригонометрического круга. Алгоритм поиска ответов очень прост:

1. Сначала стоит начертить единичную окружность.
2. Затем нужно отметить значение аркфункции аргумента правой части неравенства на дуге круга.
3. Нужно провести прямую проходящую через значение аркфункции параллельно оси абсциссы (ОХ).
4. После останется только выделить дугу окружности, являющуюся множеством решений тригонометрического неравенства.
5. Записать ответ в требуемой форме.

Разберем этапы решения на примере неравенства sin x › 1/2.  На круге отмечены точки α и β – значения

Точки дуги, расположенные выше α и β, являются интервалом решения заданного неравенства.

Если нужно решить пример для cos, то дуга ответов будет располагаться симметрично оси OX, а не OY. Рассмотреть разницу между интервалами решений для sin и cos можно на схемах приведенных ниже по тексту.

Графические решения для неравенств тангенса и котангенса будут отличаться и от синуса, и от косинуса. Это обусловлено свойствами функций.

Арктангенс и арккотангенс представляют собой касательные к тригонометрической окружности, а минимальный положительный период для обеих функций равняется π. Чтобы быстро и правильно пользоваться вторым способом, нужно запомнить на какой из оси откладываются значения sin, cos, tg и ctg.

Касательная тангенс проходит параллельно оси OY. Если отложить значение arctg a на единичном круге, то вторая требуемая точка будет расположено в диагональной четверти.  Углы

 являются точками разрыва для функции, так как график стремится к ним, но никогда не достигает.

В случае с котангенсом касательная проходит параллельно оси OX, а функция прерывается в точках π и 2π.

Целые неравенства

Неравенства по своей сути очень похожи на уравнения. Аналогично понятию целого уравнения существует понятие целого неравенства. Так называют то нер-во, в котором используются сложение и умножение, вычитание и деление, возведение в степень, но в котором нет деления на выражения с переменной. Другими словами, ни в одном знаменателе в целом нер-ве не должно быть переменных величин.

Приведем примеры целых нер-в:

14х4 + 13х2⩽ 91х3 + 2

у3 – 7 > 1/5

(z + 1)/8 <z15 + 4z9

Если бы переменная могла быть в знаменателе, то знаменатель мог бы обращаться в ноль при некоторых ее значениях, что недопустимо в математике.Но так как в целых нер-вах переменная не находиться в знаменателе, то она может принимать любое значение.

Любое целое нер-во можно преобразовать так, чтобы в одной его части (обычно правой) стоял ноль, а в другой части – некоторый многочлен Р(х).

Пример. Преобразуйте нер-во

(х3 + 7)(2х – 3) >4х(х2 – 5х + 9)

к виду Р(х) > 0, где Р(х) – это многочлен.

Решение. Раскроем скобки в каждой части нер-ва:

(х3 + 7)(2х – 3) >4х(х2 – 5х + 9)

2х4 – 3х3 + 14х – 21 > 4×3– 20х2 + 36х

Перенесем слагаемые влево и приведем подобные слагаемые:

2х4 – 3х3 + 14х – 21 – 4×3+ 20х2 – 36х > 0

2х4 – 7х3 + 20х2 – 22х – 21 > 0

Ответ:2х4 – 7х3 + 20х2 – 22х – 21 > 0

Как и в случае с уравнениями, у нер-в есть степени. Она равна степени многочлена, стоящего в одной из его частей. Так, степень неравенства в рассмотренном только что примере равна 4, ведь степень полинома 2х4 – 7х3 + 20х2 – 22х – 21 равна 4.

Замена в показательных неравенствах

Мы разобрали все виды простейших степенных неравенств. Опираясь на эти знания, можно перейти к более сложным неравенствам, которые решаются при помощи замены переменной. В ЕГЭ по профильной математике такие примеры попадаются довольно часто.

Если вы раньше решали любые уравнения или неравенства на замену переменной, то разобраться будет совсем не трудно. Давайте посмотрим на примерах:

Пример 12
$$ 4^x-29*2^x+168\le 0. $$
Согласно обычной логике в показательных неравенствах, приведем все показательные функции к одинаковому основанию. Здесь это сделать довольно легко:

$$ (2^2)^x-29*2^x+168 \le 0$$
$$ 2^{2x}-29*2^x+168 \le 0$$
Готово

Теперь обратите внимание, что \(2^{2x}=(2^x)^2\), согласно свойству степеней. Подставим:
$$ (2^x)^2-29*2^x+168 \le 0$$
В любом примере на замену переменной нужно найти одинаковые конструкции (выражения), зависящие от \(x\)

В нашем примере есть такая конструкция — \(2^x\).

Сложные тригонометрические неравенства

Если аргумент функции неравенства представлен не просто переменной, а целым выражением содержащим неизвестную, то речь уже идет о сложном неравенстве. Ход и порядок его решения несколько отличаются от способов описанных выше. Допустим необходимо найти решение следующего неравенства:

Графическое решение предусматривает построение обычной синусоиды y = sin x по произвольно выбранным значениям x. Рассчитаем таблицу с координатами для опорных точек графика:

Для простоты поиска решения заменим сложный аргумент функции

Пересечение двух графиков позволяет определить область искомых значений, при которых выполняется условие неравенства.

Найденный отрезок является решением для переменной t:

Однако, цель задания найти все возможные варианты неизвестной x:

Решить двойное неравенство достаточно просто, нужно перенести π/3 в крайние части уравнения и произвести требуемые вычисления:

Ответ на задание будет выглядеть как интервал для строгого неравенства:

Подобные задачи потребует опыта и сноровки учащихся в обращении с тригонометрическими функциями. Чем больше тренировочных заданий будет решено в процессе подготовке, тем проще и быстрее школьник найдет ответ на вопрос ЕГЭ теста.

Неравенства высоких степеней

Напомним, что если некоторое число а – корень многочлена Р(х) (то есть оно является корнем ур-ния Р(х) = 0), то этот многочлен можно представить как произведение двучлена (х – а) и какого-то другого многочлена Р₁(х). Другими словами, зная корни многочлена, можно разложить его на множители. За счет этого можно решать нер-ва высоких степеней.

Пример. Решите нер-во

х3 – 3х2 – х + 3 < 0

Решение. Найдем корни многочлена, стоящего в левой части, то есть решим ур-ние

х3 – 3х2 – х + 3 = 0

Попробуем подобрать корни, начав с целых чисел. Напомним, что все целые корни должны быть делителем свободного члена, то есть в данном случае числа 3. Поэтому «кандидатами» являются числа 1, (– 1), 3 и (– 3). Подставляя их в ур-ние, находим, что оно имеет три корня: 1, (– 1) и 3:

13 – 3•12 – 1 + 3 = 1 – 3 – 1 + 3 = 0

(– 1)3 – 3•(– 1)2 – (– 1) + 3 = – 1 – 3 + 1 + 3 = 0

33 – 3•32 – 3 + 3 = 27 – 27 – 3 + 3 = 0

Число (– 3) не подходит, ведь при его подстановке в левую часть ноль не получается:

(– 3)3 – 3•(– 3)2 – (– 3) + (– 3) = – 27 +27 + 3 + 3 = 6

Напомним, что у ур-ния 3-ей степени не может быть более 3 корней, поэтому других корней у ур-ния нет.

Зная корни, мы можем разложить многочлен на множители:

х3 – 3х2 – х + 3 = (х – 1)(х + 1)(х – 3).

В справедливости такого разложения можно убедиться, раскрыв скобки в правой части этого равенства. Теперь можно переписать исходное нер-во

х3 – 3х2 – х + 3 < 0

(х – 1)(х + 1)(х – 3) < 0

Найдем его решение методом интервалов:

Убедимся в том, что мы правильно расставили знаки, подставляя в нер-во произвольные числа из промежутков:

при х = – 2 имеем (– 2 – 1)(– 2 + 1)(– 2 – 3) = (– 3)•(– 1)•(– 5) < 0

при х = 0 получится (0 – 1)(0 + 1)(0 – 3) = (– 1)•1•(– 3) > 0

при х = 2 имеем (2 – 1)(2 + 1)(2 – 3) = 1•3•(– 1) < 0

при х = 4 получится (4 – 1)(4 + 1)(4 – 3) = 3•5•1 > 0

Получаем, что левая часть отрицательна при х∊(– ∞; – 1)∪(1; 3).

Ответ:(– ∞; – 1)∪(1; 3).

Пример. Решите нер-во

х3 + 2х – 3 > 0

Решение. Рассмотрим ур-ние

х3 + 2х – 3 = 0

Подбором можно определить лишь один его корень – единицу:

13 + 2•1 – 3 = 0

Поделим исходный многочлен на (х – 1):

Получили, что х3 + 2х – 3 = (х – 1)(х2 + 2х + 3)

Можно ли разложить на множители квадратный трехчлен х2 + 2х + 3? Попытаемся решить ур-ние

х2 + 2х + 3 = 0

D = b2– 4ас = 42 – 4•2•3 = 16 – 24 = – 8

Получили, что корней нет. Это значит, что функция у = х2 + 2х + 3 не пересекает ось Ох, и, так как коэффициент а этого трехчлена положителен, то выражение х2 + 2х + 3 больше нулю при любом х.

Это можно показать и иначе, если выделить полный квадрат из трехчлена:

х2 + 2х + 3 = х2 + 2х + 1 + 2 = (х + 1)2 + 2

Перепишем исходное нер-во с учетом разложения многочлена на множители:

х3 + 2х + 3 > 0

(х – 1)(х2 + 2х + 3) > 0

Так как выражение х2 + 2х + 3 положительно при любом значении х, то мы можем поделить неравенство на него:

х – 1 > 0

Отсюда получаем, что х∊(1; + ∞).

Ответ: (1; + ∞).

Пример. Укажите наименьшее целое решение неравенства

4х3 + 4х2 – 7х + 2 > 0

Решение. Попытаемся найти корень многочлена 4х3 + 4х2 – 7х + 2. Целый корень должен быть делителем двойки (свободного члена), то есть возможны варианты 1 и (–1), 2 и (– 2). Из них подходит только – 2:

4•(– 2)3 + 4•(– 2)2 – 7•(– 2) + 2 = – 32 + 16 + 14 + 2 = 0

Значит, можно поделить исходный многочлен на х + 2:

Можно записать, что 4х3 + 4х2 – 7х + 2 = (х + 2)(4х2 – 4х + 1).

Далее разложим получившийся при делении квадратный трехчлен на множители, для чего приравняем его к нулю:

4х2 – 4х + 1 = 0

D = b2– 4ас = (– 4)2 – 4•4•1 = 16 – 16 = 0

Получается, что есть лишь один корень.

х = – b/(2a) = – (– 4)/(2•4) = 0,5

Если у квадратного трехчлена дискриминант равен нулю, то это значит, что он является полным квадратом какого-то выражения. Действительно:

4х2 – 4х + 1 = (2х)2 – 2•2х•1 + 12 = (2х – 1)2

Тогда можно записать:

4х3 + 4х2 – 7х + 2 = (х + 2)(4х2 – 4х + 1) = (х + 2)(2х – 1)2 =

= (х + 2)(2х – 1)(2х – 1)

Перепишем с учетом этого исходное нер-во:

4х3 + 4х2 – 7х + 2 > 0

(х + 2)(2х – 1)(2х – 1) > 0

Вынесем множитель 2 из двух последних скобок и поделим нер-во на них:

(х + 2)•2•(х – 0,5)•2•(х – 0,5) > 0

(х + 2)(х – 0,5)(х – 0,5) > 0

Решим его методом интервалов:

Снова из-за двух одинаковых скобок (х – 0,5) на соседних промежутках (– 2; 0,5) и (0,5; 2) получили один и тот же знак. Функция положительна на них, однако она равна нулю при х = 0,5, поэтому это число из решения неравенства исключается. Получаем, что х∈(– 2; 0,5)∪(0,5; + ∞).

Нам надо указать наименьшее целое решение. Самым малым целым числом из множества (– 2; 0,5)∪(0,5; + ∞) является (– 1).

Ответ: (– 1).

ОДЗ (Область допустимых значений)

Помнишь, что такое ОДЗ?

Например, в уравнении \( \sqrt{x+2}=3\) присутствует квадратный корень. А квадратный корень не имеет смысла, если подкоренное выражение отрицательно.

То есть, в данном случае ОДЗ – это решения неравенства \( x+2\ge 0\).

Нет необходимости искать ОДЗ в каждой задаче, содержащей корень.

Взять, например, такую задачу:

\( \sqrt{{{x}^{2}}+3x}>2\).

При возведении в квадрат получаем \( {{x}^{2}}+3x>4\), то есть подкоренное выражение автоматически неотрицательно! Так зачем лишняя писанина?

Но в некоторых случаях это может быть очень полезно. Более того, иногда можно решить пример, просто найдя ОДЗ. Например:

\( \sqrt{2{x}-6}>-2\).

Но ведь мы помним, что квадратный корень всегда неотрицателен. Поэтому он всегда будет больше \( -2\). Значит, решением задачи будет ОДЗ:

\( 2{x}-6\ge 0\text{ }\Leftrightarrow \text{ }x\ge 3\).

Неравенства второй степени

Неравенства второй степени в общем виде записываются так:

ах2 + bx + c> 0

Примерами таких нер-в являются

5х2 – 3х + 19 > 0

– 12у2 + 1,23у + 64 ⩾ 0

462z2 + 3z– 54 < 0

В левой части такого нер-ва стоит квадратичная функция. Вспомним два важных момента:

1. Ветви параболы у = ах2 + bx + c смотрят вверх, если коэффициент а > 0, и смотрят вниз, если а < 0.
2. Чтобы найти нули функции у = ах2 + bx + c, надо решить квадратное ур-ние ах2 + bx + c = 0. Если его дискриминант (D) больше нуля, то есть два нуля. Если D = 0, то есть только один ноль. Если D< 0, то парабола не пересекает ось Ох.

В соответствии с этим возможно 6 случаев расположения графика квадратичной функции на координатной плоскости, в зависимости от значений старшего коэффициента a и дискриминанта D:

При решении нер-в 2-ой степени обязательно возникает один из этих случаев. Поэтому для решения нер-ва

ах2 + bx + c> 0

надо решить ур-ние ах2 + bx + c = 0 и проанализировать положение графика квадратичной функции относительно оси Ох.

Пример. Найдите промежуток, на котором справедливо нер-во

2х2 – 5х + 2 < 0

Решение. Найдем корни ур-ния 2х2 – 5х + 2 = 0.

D = b2– 4ас = (– 5)2 – 4•2•2 = 25 – 16 = 9

х₁ = (5 – 3)/4 = 0,5

х₂ = (5 + 3)/4 = 2

Коэффициент а параболы положителен, поэтому ее ветви смотрят вверх. Сам график будет выглядеть так:

Однако нам достаточно и схематичного изображения параболы и ее нулей на координатной прямой:

Нули функции разбивают прямую на три промежутка. На каждом из них знак квадратичной функции неизменен. Отметим эти знаки:

В нер-ве стоит знак «<». Значит, нам нужен промежуток от 0,5 до 2, на котором ф-ция отрицательна (парабола ниже оси Ох). Нер-во строгое, а потому сами числа 0,5 и 2 не входят в промежуток. Такие «выколотые точки» обозначают белыми кружочками:

Ответ: (0,5; 2)

Пример. Решите нер-во

– 2х2 + 9х – 9 ≤ 0

Решение. Сначала находим нули параболы, решая ур-ние

– 2х2 + 9х – 9 = 0

D = b2– 4ас = 92 – 4•(– 2)•(– 9) = 81 – 72 = 9

х₁ = (– 9 – 3)/ (– 4) = 3

х₂ = (– 9 + 3)/ (– 4) = 1,5

Коэффициент а параболы отрицательный, поэтому ее ветви смотрят вниз. Отметим на координатной прямой нули ф-ции и схематично график параболы, а также промежуток, на котором она неположительна:

Так как нер-во нестрогое, то сами нули ф-ции входят в ответ, а потому скобки рядом с нулями – квадратные. В итоге х∊(– ∞; 1,5]∪[3; + ∞).

Ответ: х∊(– ∞; 1,5]∪[3; + ∞).

Пример Решите нер-во

х2 – 2х + 1 > 0

Решение. Решим квадратное ур-ние

х2 – 2х + 1 = 0

D = b2– 4ас = (– 2)2 – 4•1•1 = 4 – 4 = 0

Дискриминант равен нулю, поэтому у ур-ния лишь 1 корень.

х₁ = – b/2a = – (– 2)/2 = 1

Парабола будет касаться прямой Ох в единственной точке, при этом ветви параболы должны смотреть вверх:

Получается, что ф-ция положительна на всей координатной прямой, кроме точки х = 1, где она обращается в ноль. Соответственно, в ответе надо указать объединение промежутков: х∊(– ∞; 1)∪(1; + ∞).

Ответ: (– ∞; 1)∪(1; + ∞).

Пример. Найдите решение нер-ва

– 5х2 + х – 100 < 0

Решение. Попытаемся найти корни ур-ния

– 5х2 + х – 100 = 0

D = b2– 4ас = 12 – 4•(– 5)•(– 100) = 1 – 2000 = – 2001

Дискриминант меньше нуля, поэтому корней не будет. Вся парабола будет находиться ниже оси Ох, так как ее ветви должны смотреть вниз из-за отрицательного коэффициента а = – 5.

Видно, что при любых значениях х левая часть нер-ва меньше нуля, то есть нер-во справедливо при х∊(– ∞; + ∞).

Ответ: (– ∞; + ∞).

Основные понятия

Алгебра не всем дается легко с первого раза

Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства

Неравенство — это алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.

Линейные неравенства — это неравенства вида:

• ax + b < 0,
• ax + b > 0,
• ax + b ≥ 0,
• ax + b ≤ 0,

где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье. 

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти все значения переменной, при которой неравенство верное.

Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Пройти урок