Тайны пирамиды (теория чисел и не только) - математика

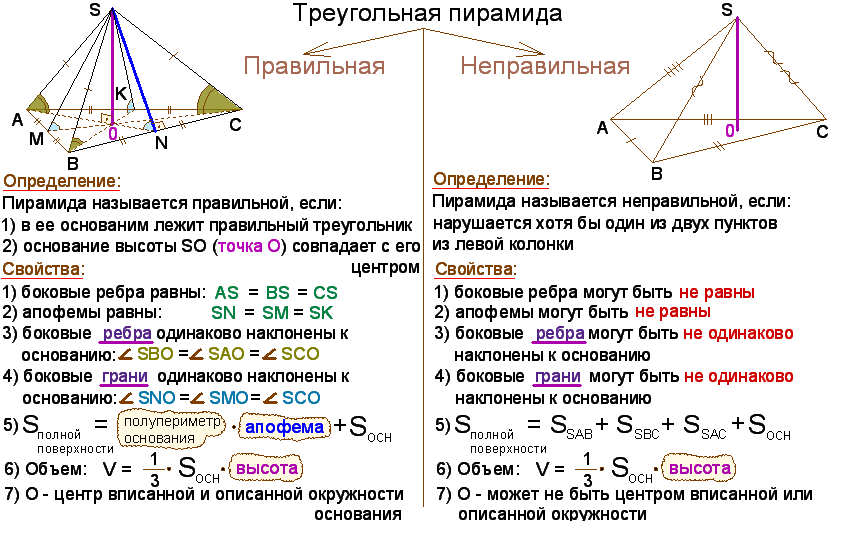
Цифровая пирамида числа треугольников

s http-equiv=»Content-Type» content=»text/html;charset=UTF-8″>tyle=»clear:both;»>

Рассмотрим цифровые пирамиды, отображаемые ниже. Напишите программу для расчета максимального количества путей, которые заканчиваются внизу в самой высокой точке внизу. Каждый шаг может быть достигнут до точки внизу слева.

        7 
      3   8 
    8   1   0 
  2   7   4   4 
4   5   2   6   5

В приведенных выше образцах путь от 7 до 3 до 7 до 7 до 5 дал максимальную сумму: 30

Input

Первая строка содержит R (1 <= r <= 1000), что означает количество строк. Каждое поведение, стоящее за этой цифровой пирамидой, включено. Все поставляемое целое число не является негативным и не превышающим 100.

Divis dp, вы можете взять линию, чтобы справиться с одной линией

Интеллектуальная рекомендация

Новый проект- исходный файл. Найдите свой файл .cpp. Прямая картина Значение этой операции заключается в том, что текущий основной файл CPP не вступает в силу. Следовательно, во -первых, все файлы CPP…

Ты мои глаза, ведущие меня по бесконечным дорогам. Лидар, ведущие беспилотные автомобили к дальнейшему развитию Принцип лидара — это активное устройство дистанционного зондирования, в котором в качест…

Ограничение тока потребителя Зачем нужен лимит тока со стороны потребителя? Предположим, что у нашего сервера Rabbitmq есть десятки тысяч необработанных сообщений, мы просто открываем клиентского клие…

Используйте облачную платформу IAAS для создания облачного хоста Процесс работы создания облачного хоста Используйте облачную платформу IAAS для создания облачного хоста * Создать внешнюю сеть * Созда…

Сканер — это инструмент, который автоматически выполняет пакетный поиск информации на веб-страницах. Принцип работы можно кратко описать так: Сканер переходит к группе предварительно оцененных веб-сай…

Вам также может понравиться

Случайное случайное число Массив длины 10 на элемент массива может разместить значение 0-15, используя NUM = New Random (). Nextint (15) инициализирует массив, определить, есть ли тот же элемент в…

Такая строка появляется при использовании Hadoop или других команд: Bash: Hadoop: Команда не Fount Решение: $ gedit /etc/profile После входа в редактор добавьте путь Hadoop: export HADOOP_HOME=/opt/ha…

…

Примечание. После использования NGINX он чувствует себя очень удобно после личного использования, поэтому я даю себе решение для установки и конфигурации. Это высокопроизводительный веб -сервер и прок…

Выполнить кэш NPM Clean -force Очистка кеша Выполните NPM Install-Global Vue-Cli снова Если вы все еще потерпите неудачу, вы будете https://www.jianshu.com/p/0d178b016d55 Тогда я преуспе…

Усечённая пирамида

Возьмем произвольную пирам-у, а далее секущую плоскость, которая будет параллельна основанию, причем она будет пересекать ребра РА₁, РА₂, РА₃… в точках В₁, В₂, В₃… соответственно. В результате, отбросив «верхушку» пирам-ы, мы получим новую фигуру, которая именуется усеченной пирамидой.

У усеченной пирам-ы уже не одна, а две грани считаются основаниями, и они параллельны друг другу. Большее из них именуют нижним основанием, а меньшее – верхним основанием.

Докажем, что боковые грани любой усеченной пирам-ы – это трапеции. Действительно, обозначим плос-ть верхнего основания как α, нижнее основание как β, а произвольную грань как γ:

Нам надо доказать, что А₁А₂В₂В₁ – это трапеция. Действительно, прямые А₁А₂ и В₁В₂ не могут скрещиваться, ведь они располагаются в единой плос-ти γ. Не могут они и пересекаться, ведь тогда точка их пересечения была бы общей для плос-тей α и β, а эти плос-ти параллельны. Остается один вариант: А₁А₂||В₁B₂. Две другие стороны грани, А₁В₁ и А₂В₂, будут пересекаться в точке Р, вершине исходной пирам-ы. Тогда по определению две четырехугольник А₁А₂В₂В₁ будет трапецией, ведь у него две стороны параллельны, а две другие – нет.

Отдельно отметим, что усеченная пирам-а, полученная из правильной пирам-ы, также называется правильной, а высоты ее боковых граней также именуются апофемами. Докажем одну теорему:

Действительно, пусть из правильной пирам-ы с вершиной в Р получена правильная усеченная пирамида с основаниями А₁А₂А₃…A_n и В₁В₂В₃…B_n:

Так как исходная пирам-а – правильная, то ее грани – равные равнобедренные треугольники, у которых одинаковы углы при основаниях:

Мы уже знаем, что грани А₁А₂В₂В₁ и А₂А₃В₃В₂ – трапеции. Раз у них одинаковы углы при основании, то можно утверждать, что эти трапеции – равнобедренные. Это значит, что любые два боковых ребра, находящиеся на одной грани, одинаковы. Значит, одинаковы вообще все боковые ребра. Получается, что все боковые грани – это равнобедренные трапеции с одинаковыми основаниями, боковыми сторонами и углами при основании. Этого достаточно для того, чтобы считать эти трапеции равными, ч. т. д.

Из этой теоремы вытекает тот факт, что стороны многоуг-ка, образующего верхнее основание, одинаковы. Более того, углы этого многоуг-ка равны таким же углам в нижнем основании. Например, ∠А₁А₂А₃ = ∠В₁В₂В₃. Действительно, мы знаем, что А₁А₂||В₁В₂ и А₂А₃||B₂B₃, и потому стороны углов ∠А₁А₂А₃ = ∠В₁В₂В₃ оказываются сонаправленными лучами.

Так как в нижнем многоуг-ке А₁А₂А₃…A_n все углы одинаковы (ведь он правильный), то и в верхнем многоуг-ке В₁В₂В₃…B_n также будут одинаковы углы. В итоге можно утверждать, что верхнее основание усеченной пирамиды является правильным многоуг-ком, также как и нижнее.

Отметим ещё один факт. При построении секущей плос-ти пирам-а делится на две части. Нижняя из них – это усеченная пирам-а, а верхняя – это обычная пирам-а, меньшая исходной. Докажем, что если исходная пирам-а РА₁А₂А₃…Р_n была правильной, то оставшаяся после отсечения «верхушка» также будет правильной пирам-ой. Мы уже выяснили, что ее основание В₁В₂В₃…В_n– правильный многоуг-к. Отрезки РА₁, РА₂, РА₃… одинаковы как боковые ребра исходной правильной пирам-ы. В свою очередь отрезки А₁В₁, А₂В₂, А₃В₃ одинаковы как боковые ребра правильной усеченной пирам-ы. Но отсюда получается, что одинаковы также и отрезки РВ₁, РВ₂, РВ₃… Значит, в пирам-е РВ₁В₂В₃…В_n в основании лежит правильный многоуг-к, а ее боковые ребра одинаковы. Из этого вытекает, что эта пирам-а – правильная.

Ещё одна теорема позволяет вычислять площадь боковой поверхности правильной усеченной пирам-ы:

Действительно, каждая грань такой пирам-ы – это трапеция. Обозначим длину ее верхнего основания буквой а, а нижнего – буквой b.Тогда, если основания пирам-ы – это многоуг-ки с n сторонами, периметр этих оснований будет вычисляться так:

Теперь проведем на каждой боковой грани апофему, чья длина будет обозначаться как d. Тогда, используя формулы площади трапеции, сможем вычислить площадь грани:

Что ответить на вопрос У меня 6 яиц?

У меня 6 яиц: ответ

Пояснение: Ответ шесть из-за использования прошедшего и настоящего времени в загадке. В загадке говорится, что у вас есть 6 яиц, в которых используется настоящее предложение. Затем следует, что вы разбили, приготовили и съели несколько яиц.

Какой ответ на загадку, если бы у меня было 4 яйца?

В то время как общий ответ на это был угадан как 7, 4 и 1, правильный ответ на загадку 3 яиц
. Хитрость в решении этой загадки заключается в том, чтобы понять, что это не математическая задача, а простая игра слов, которая сбивает людей с толку.

Как решить головоломку из двух частей пирамиды?

Как сделать трехгранную пирамиду из дерева? Оглавление Скрыть

Шаг 1: Измерьте размеры треугольника пирамиды, выбрав размер и размер.
Шаг 2: Соедините стороны треугольника длинными сторонами с основанием, чтобы получились четыре стороны пирамиды.
Шаг 3: Склейте все стороны, используя столярный клей, чтобы закрепить структуру пирамиды.

Как начертить пирамиду в прямоугольной системе координат?

14) Выполним точный чертёж пирамиды прямоугольной системе координат. Это проще, чем кажется.

С чего начать?

Во-первых, необходимо уметь правильно изображать саму систему координат на клетчатой бумаге. Справка в начале методички Графики и свойства функций.

Во-вторых, необходимо уметь строить точки в трёхмерном пространстве, об этом я уже начал рассказывать в статье Уравнения прямой в пространстве. И сейчас мы продолжим тему.

Построим точку . На мой взгляд, сначала удобно разобраться с первыми двумя координатами – «иксом» и «игреком»: отмеряем 2 единицы в положительном направлении оси и 3 единицы в отрицательном направлении оси . В плоскости прочерчиваем пунктирные дорожки, которые параллельны соответствующим координатным осям. Пересечение дорожек я пометил небольшим ромбиком:

Теперь, в соответствии с отрицательной «зетовой» координатой, отмеряем 1 единицу вниз и тоже проводим пунктирную дорожку. Здесь и будет находиться наша точка , она расположена в нижнем полупространстве.

Для точки отмеряем 5 единиц «на себя» и 4 единицы вправо, строим параллельные осям пунктирные дорожки и находим их точку пересечения. В соответствии с «зетовой» координатой, чертим пунктиром «подставку для точки» – 2 единицы вверх. Данная точка расположена в верхнем полупространстве.

Аналогично строятся две другие точки. Заметьте, что вершина лежит в самой плоскости .

В тетради пунктирные линии аккуратно и не жирно проводятся простым карандашом.

Теперь нужно разобраться в удалённости точек, а в этом как раз и помогут пунктирные линии. Немного включаем пространственное воображение и внимательно смотрим на ось . Очевидно, что самая близкая к нам вершина – , а самая удалённая – .

Немало читателей уже мысленно прорисовали пирамиду, тем не менее, остановлюсь на построении подробнее. После того, как построены вершины, чайники могут тонко-тонко карандашом начертить все 6 сторон, и начинать разбираться, какие рёбра видимы, а какие рёбра скрыты. Лучше начать от самой близкой точки . Очевидно, что все три «исходящих» ребра в поле нашего зрения:

Должен предостеречь, так бывает далеко не всегда, одно ребро, например, может быть от нас скрыто. Не теряйте визуального восприятия пространства!

Какие ещё стороны в зоне видимости? ВиднЫ рёбра , а вот сторона спряталась за пирамидой:

К слову, невидимое нам ребро лежит в нижнем полупространстве и проходит под осями .

Чертеж-конфетка на практике получается не во всех случаях. Бывает, фортуна разворачивается и задом:

То есть, грань пирамиды может полностью или частично закрывать всё остальное. Но самое скверное, когда перекрываются рёбра:
Тут сразу три ребра выстроились на одной прямой (правая верхняя прямая). В похожей ситуации приходится жирно прочерчивать накладывающиеся стороны разными цветами и ниже чертежа записывать дополнительные комментарии о расположении пирамиды.

Существуют и более мелкие неприятности, например, одна из сторон пирамиды может наложиться на координатную ось (а то и вовсе расположиться за ней).

Увы, перечисленные случаи – не редкость на практике.

Вот, пожалуй, и все основные сведения о построении треугольной пирамиды в декартовой системе координат.

15) Это пример для самостоятельного решения.

В конце решения желательно ~~остограммиться~~ записать ответ, и по пунктам перечислить полученные результаты. За ваше здоровье!

(Переход на главную страницу)

Какая самая старая женщина имеет менструальный цикл?

Средний возраст наступления естественной менопаузы составлял 50.9 года. Самые старые менструирующие женщины были 57 Ваш старый.

Можно ли забеременеть в 44 года?

По данным Центров по контролю и профилактике заболеваний (CDC), 30% женщин в возрасте 40 и 44 страдают бесплодием. 1 Ваши шансы на зачатие в любом конкретном месяце также снижаются по мере того, как вы становитесь старше. Каждый месяц средняя 30-летняя женщина имеет около 20% шансов забеременеть.

Почему яйца вредны для самок? Яйца также загружены холестерин— около 200 миллиграммов на яйцо среднего размера. Это более чем вдвое больше, чем у Биг Мак. Жир и холестерин способствуют развитию сердечных заболеваний. Исследование 2021 года показало, что добавление половины яйца в день было связано с большим количеством смертей от болезней сердца, рака и всех причин.

Как работают пирамиды сложения?

Как работают эти пирамиды? Сложите 2 числа рядом друг с другом в ряд и напишите ответ в кружке над этими 2 числами.. Сложите все соседние числа в каждой строке. … Теперь складывайте эти числа, пока не заполните все ряды и не достигнете вершины пирамиды.

тогда Сколько яиц в головоломке пирамиды? 13 коричневых яиц все поддерживают друг друга на картинке, чтобы сделать пирамиду. Я надеюсь, что это поможет с вопросом яйца. Не волнуйтесь, пока есть достаточно бекона и печенья с соусом из колбасы, чтобы пойти с ними. Ответ на все эти загадки заключается в том, чтобы искать подвох.

Как сделать пирамиду из двух частей? Деревянная головоломка-пирамида из двух частей

Шаг 1: Что вам нужно: — Ленточная пила. – Наждачная бумага. …
Шаг 2: Вырежьте 1 и 2. – Разрежьте кусок дерева на две части размером 1 1/8″ x 1 3/8″ x 2 3/4″. …
Шаг 3: Отрежьте 3 и 4. – Нарисуйте линию по центру одной из граней шириной 1 3/8″ на одном блоке. …
Шаг 4: Шлифовка. – Отшлифуйте все грани каждой детали.

Правильная пирамида

Особый интерес и в геометрии, и в реальной жизни представляют так называемые правильные пирамиды. Их отличают две особенности:

1) в их основании находится правильный многоугольник;

2) высота пирам-ы падает на основание в точке, являющейся центром этого правильного многоуг-ка.

Напомним, что центром правильного многоуг-ка считается центр описанной около него окружности, который одновременно является и центром вписанной окружности.

Действительно, опустим из вершины Р правильной пирам-ы высоту РО. Тогда О будет центром описанной окружности:

Примечание. На рисунках, показывающих объемные фигуры, окружности искажают свою форму и выглядят как эллипсы, то есть овалы.

Построим из О радиусы ОА₁, ОА₂, ОА₃,… Они все будут одинаковы, ведь это радиусы одной и той же окружности. Также заметим, что высота правильной пирамиды РО будет перпендикулярна каждому из этих радиусов, ведь она перпендикулярна и всей плос-ти. Это значит, что ∆РОА₁, ∆РОА₂, ∆РОА₃… – прямоугольные. При этом у них есть общий катет РО, а катеты ОА₁, ОА₂, ОА₃… одинаковы. Значит, эти треугольники равны. Отсюда и вытекает, что их гипотенузы, то есть боковые ребра РА₁, РА₂, РА₃…, также одинаковы, ч. т. д.

Заметим, что можно доказать и почти противоположное утверждение – если у пирам-ы боковые ребра одинаковы, а в основании находится правильный многоуг-к, то она является правильной. Для доказательства предположим, что ребра РА₁, РА₂, РА₂… одинаковы. Опустим из Р высоту, которая упадет в некоторую точку О. Теперь соединим эту точку с вершинами А₁, А₂, А₃… Получатся прямоугольные ∆РОА₁, ∆РОА₂, ∆РОА₃… У них есть общий катет (высота РО) и одинаковые гипотенузы. Значит, эти треугольники равны, и потому одинаковы отрезки ОА₁, ОА₂, ОА₃… Это значит, что точка О равноудалена от вершин многоуг-ка, и если из нее провести окружность радиусом ОА₁, то она также пройдет через остальные вершины многоуг-ка. То есть эта окружность окажется описанной. Это и означает, что точка О – центр многоуг-ка, и тогда вся пирам-а оказывается по определению правильной.

Из равенства боковых ребер напрямую вытекает и тот факт, что все боковые грани правильной пирам-ы – одинаковые равнобедренные треугольники. Высоты, проведенные в этих равнобедренных треугольниках к основанию правильной пирамиды, именуются апофемами.

Ещё раз уточним, что понятие апофемы применимо только к правильной пирам-е. У других пирамид тоже можно на боковых гранях провести высоты к основанию, но они просто не будут называться апофемами пирамиды.

Ясно, что раз в правильной пирам-е все боковые грани – равные друг другу равнобедренные треуг-ки, то и их высоты, то есть апофемы, одинаковы. Также можно утверждать, что каждая апофема делит ребра, на которое она падает, пополам, ведь высоты в равнобедренном треуг-ке – это ещё и медианы.

Апофема используется для вычисления площади боковой поверхности пирам-ы, так как существует такая теорема:

Докажем ее. Пусть у правильной n-угольной пирам-ы в основании находится многоуг-к со стороной а. Тогда его периметр Р вычисляется так:

Каждая боковая грань пирам-ы – это треугольник. Проведем на них апофемы, которые одновременно окажутся и высотами для этих треугольников. Если мы обозначим длину апофемы как d, то площадь каждой грани можно рассчитать по простейшей формуле площади треугольника:

Какая фигура должна стоять на вершине пирамиды?

От наименьшего к большинству: наименьшее количество элементов вверху и наибольшее количество внизу. Например, пищевая пирамида Министерства сельского хозяйства США показывает, что жиры, масла и сладости (вверху, в самом маленьком куске) следует есть меньше, чем другие продукты в более крупных частях внизу, таких как хлеб, хлопья, рис и макароны (внизу, в самом большом куске).

Что является примером пирамиды чисел? Например, жирный сидеть на низшем трофическом уровне или в основании числовой пирамиды из-за их обилия. Основной потребитель, такой как кузнечик, занимает следующий более высокий трофический уровень. Кузнечиков меньше, чем травы.

Что такое пирамида умножения?

Что такое пирамида умножения? Пирамиды умножения пирамиды чисел. В пирамиде умножения числа, расположенные рядом друг с другом (множители), умножаются, чтобы получить число над ним. Результат каждой операции умножения называется произведением.

Когда рождается самка, у нее рождается сколько яиц? Со сколькими яйцеклетками рождаются женщины? Будучи плодом на ранней стадии развития, самка имеет около колоссальных 6 миллионов яиц. Количество этих яйцеклеток (точнее, ооцитов) неуклонно уменьшается, так что, когда рождается девочка, у нее от 1 2 до XNUMX миллионов яиц.

Числовые пирамиды

В следующих витринах галереи нас поражают числовые достопримечательности совсем особого рода — некоторое подобие пирамид, составленных из чисел, Рассмотрим поближе первую из них:

        1 X 9 + 2 = 11 
       12 X 9 + 3 = 111 
      123 X 9 + 4 = 1111 
     1234 X 9 + 5 = 11111 
    12345 X 9 + 6 = 111111 
   123456 X 9 + 7 = 1111111 
  1234567 X 9 + 8 = 11111111 
 12345678 X 9 + 9 = 111111111

Как объяснить эти своеобразные результаты умножения?

Чтобы постичь эту странную закономерность, возьмем для примера какой-нибудь из средних рядов нашей числовой пирамиды: 123456 X 9 + 7. Вместо умножения на 9 можно умножить на (10 — 1), то-есть приписать 0 и вычесть умножаемое:

Достаточно взглянуть на последнее вычитание, чтобы понять, почему тут получается результат, состоящий только из одних единиц.

Мы можем уяснить себе это, исходя и из других рассуждений. Чтобы число вида 12345… превратилось в число вида 11111…, нужно из второй его цифры вычесть 1, из третьей — 2, из четвертой — 3, из пятой — 4 и т. д. — иначе говоря, вычесть из него то же число вида 12345…, вдесятеро уменьшенное и предварительно лишенное последней цифры. Теперь понятно, что для получения искомого результата нужно наше число умножить на 10, прибавить к нему следующую за последней цифру и вычесть из результата первоначальное число (а умножить на 10 и отнять множимое — значит умножить на 9).

Сходным образом объясняется образование и следующей числовой пирамиды, получающейся при умножении определенного ряда цифр на 8 и прибавлении последовательно возрастающих цифр:

         1 X 8 + 1 = 9 
        12 X 8 + 2 = 98 
       123 X 8 + 3 = 987 
      1234 X 8 + 4 = 9876 
     12345 X 8 + 5 = 98765 
    123456 X 8 + 6 = 987654 
   1234567 X 8 + 7 = 9876543 
  12345678 X 8 + 8 = 98765432 
 123456789 X 8 + 9 = 987654321

Особенно интересна в пирамиде последняя строка, где в результате умножения на 8 и прибавления 9 происходит превращение натурального ряда цифр в таковой же ряд, но с обратным расположением. Объясним эту особенность.

Получение странных результатов уясняется из следующей строки:

1 ()

то-есть 12345 X 8 + 5 = 111111 — 12346. Но, вычитая из числа 111111 число 12346, составленное из ряда возрастающих цифр, мы, как легко понять, должны получить ряд убывающих цифр: 98765.

Вот наконец третья числовая пирамида, также требующая объяснения:

        9 X 9 + 7 = 88 
       98 X 9 + 6 = 888 
      987 X 9 + 5 = 8888 
     9876 X 9 + 4 = 88888 
    98765 X 9 + 3 = 888888 
   987654 X 9 + 2 = 8888888 
  9876543 X 9 + 1 = 88888888 
 98765432 X 9 + 0 = 888888888

Эта пирамида является прямым следствием первых двух. Связь устанавливается очень легко. Из первой пирамиды мы знаем уже, что, например:

12345 X 9 + 6 = 111111.

Умножив обе части на 8, имеем:

(12345 X 8 X 9) + (6 X 8) = 888 888.

Но из второй пирамиды известно, что

12345 X 8 + 5 = 98765, или 12345 X 8 = 98760.

Значит:

888888 = (12345 X 8 X 9) + (6 X 8) = (98760 X 9) + 48 = (98760 Х 9) + (5 Х 9) + 3 = (98760 + 5) Х 9+ 3 = 98765 X 9 + 3.

Вы убеждаетесь, что все эти числовые пирамиды не так уж загадочны, как кажутся с первого взгляда.

Гадание Числовая пирамида

Существует огромное множество видов гадания: гадания на Таро, гадания на кофейной гуще, на астрологических символах. Некоторые из них являются довольно сложными и требуют определённых навыков, например, предсказания с помощью положения планет на небосводе, некоторые являются даже опасными, как например, предсказания, связанные с вызыванием духов. Есть и очень простые гадания, такие как гадание на монетке. Числовая пирамида относится к довольно простым и безопасным методам гаданий, и к тому же требует совсем немного времени.

Метод гадания Числовая пирамида

Необходимо правильно задать вопрос, так, чтобы второе слово всегда было «ли». Например, «выйдет ли Иванова Наталья замуж за Семёнова Семёна?».

Теперь необходимо сосчитать количество букв в каждом слове вопроса и написать эти числа вряд. Получается, «выйдет» — 6, «ли» — 2, «Иванова» — 7, «Наталья» — 7, «замуж» — 5, «за» — 2, «Семенова» — 8, «Семена» — 6.

Если количество букв в слове превышает 9, то нужно сложить цифры в числе, и записать результат. Например, количество букв в слове равно 12, 1 складывается с 2, получаем 3, которое записывается в ряду.

Далее необходимо сложить первое и второе число, а результат записать под ними. 6 плюс 2 даёт 8. Потом складывается второе и третье числа, а результат записывается под ними. 2 плюс 7 равняется 9. То же самое необходимо сделать с третьим и четвёртым числами, с четвёртым и пятым, и т.д.

Если сумма чисел превышает 9, то необходимо сложить цифры, составляющие число и записать результат. Как в примере, 7 плюс 7 даёт 14, 14 больше 9, поэтому нужно сложить цифры 1 и 4, и полученный результат 5 записывается под 7 и 7.

Такую процедуру необходимо проделать со всеми числами первого ряда, пока не получится новый ряд чисел под ним. Количество чисел во втором ряду должно быть на единицу меньше, чем в первом.

Теперь необходимо проделать ту же самую процедуру с числами второго ряда, записывая результаты внизу. Первое число второго ряда складывается со вторым числом второго ряда и результат записывается под ними, образуя первое число третьего ряда.

Так получается третий ряд, количество цифр в котором будет на одну меньше, чем в предыдущем ряду.

Такое сложение необходимо проводить до тех пор, пока в последнем ряду не окажется одна единственная цифра.

Эта цифра и будет ответом на вопрос.

Так как все записанные друг под другом ряды образуют собой перевёрнутую пирамиду из цифр, в вершине которой является ответ, то гадание поэтому и носит название Числовая пирамида.

Интерпретации ответа

В этом гадании возможно только девять вариантов ответа, поэтому, как и во множестве других гаданий, необходимо прибегнуть к помощи интуиции, чтобы ответ стал более ёмким. Ниже приводятся расшифровка ответов по полученным цифрам в вершине пирамиды.

Как решить головоломку с деревянной пирамидой?

Как читать пирамидальную диаграмму? Пирамидальная диаграмма

Ширина каждой секции варьируется от наименьшей на вершине пирамиды до увеличения по мере продвижения к основанию пирамиды. Тема помещается в каждый раздел пирамидальной диаграммы. Ширина каждого раздела показывает уровень иерархии тем.

Что общего у пирамид и призм?

Сходства: общие черты

Призмы и пирамиды — три-мерные твердые формы, содержащие стороны и грани то есть многоугольники — двумерные фигуры с прямыми сторонами. Обе формы подпадают под большую категорию — многогранники — потому что стороны и основания являются многоугольниками.

Какие существуют три типа пирамид? Экологические пирамиды показывают относительное количество энергии или вещества, содержащихся на каждом трофическом уровне в данной пищевой цепи или пищевой сети. Три разных типа Пирамиды энергии, биомассы и чисел.

Почему пирамида чисел перевернута?

Пирамида числа указывает количество особей на каждом трофическом уровне. Пирамида числа перевернута в древесной экосистеме. В этом, первый трофический уровень содержит наименьшее количество деревьев. Насекомые, питающиеся первичным продуцентом, занимают второй трофический уровень.

Как решить лестницу умножения?

Как решить умножение арифмагона?

Возраст от 14 до 16

Существует метод решения арифмагонов умножения, который работает каждый раз. Сначала вы умножаете все числа в красных прямоугольниках, а затем находите квадратный корень.. Это позволит найти произведение всех чисел в полях с фиолетовой рамкой.

Как называется результат умножения? Результат операции умножения называется продукт. Умножение целых чисел можно рассматривать как многократное сложение; то есть умножение двух чисел эквивалентно добавлению такого количества копий одного из них, множимого, как количество другого, множителя.