Пояснения к калькулятору
- Для решения математического выражения необходимо набрать его в поле ввода с помощью предложенной виртуальной клавиатуры и нажать кнопку ↵.
- Управлять курсором можно кликами в нужное местоположение в поле ввода или с помощью клавиш со стрелками ← и →.
- ⌫ — удалить в поле ввода символ слева от курсора.
- C — очистить поле ввода.
- При использовании скобок ( ) в выражении в целях упрощения может производится автоматическое закрытие, ранее открытых скобок.
- Для того чтобы ввести смешанное число или дробь необходимо нажать кнопку ½, ввести сначала значение числителя, затем нажать кнопку со стрелкой вправо → и внести значение знаменателя дроби. Для ввода целой части смешанного числа необходимо установить курсор перед дробью с помощью клавиши ← и ввести число.
- Ввод числа в n-ой степени и квадратного корня прозводится кнопками ab и √ соответственно. Завершить ввод значения в степени или в корне можно клавишей →.
Photomath — решает математические задачи по фото
И первое из приложений, которые мы рассмотрим — Photomath. Очень удобное и занимает топ по скачиванию из магазинов. Помогает не разочаровываться в математике и понять задачи из различных областей. Решает: квадратные уравнения, логарифмы, задачи по тригонометрии, интегральные исчисления и другое.
Итак, давайте рассмотрим как им пользоваться.
- Для начала скачиваем его в Play Market или App Store.
- После чего предлагают выбрать язык, если что его можно сменить в любое время. И кем вы являетесь: ученик, родитель, учитель.
- После быстрой регистрации, нам открывается камера с окошком, под которое нужно подставить уравнение. На панели справа можете заметить фонарик, его можно включить, если вы в темноте фотографируете. Снизу калькулятор, где можно ввести все вручную.
- Мы навели камеру на рандомное уравнение из интернета и вот какой получился ответ.
- Что нам показалось самым удобным — это то, что впоследствии есть последовательность решения. Не просто ответ, непонятно откуда взятый. Например, если вас спросят: «А как ты это сделал?». Можно пошагово показать схему действий.
Конечно же рекомендуем вам им воспользоваться. Во-первых, удобное и простое. Во-вторых, шикарный дизайн и шрифт, приятно пользоваться.
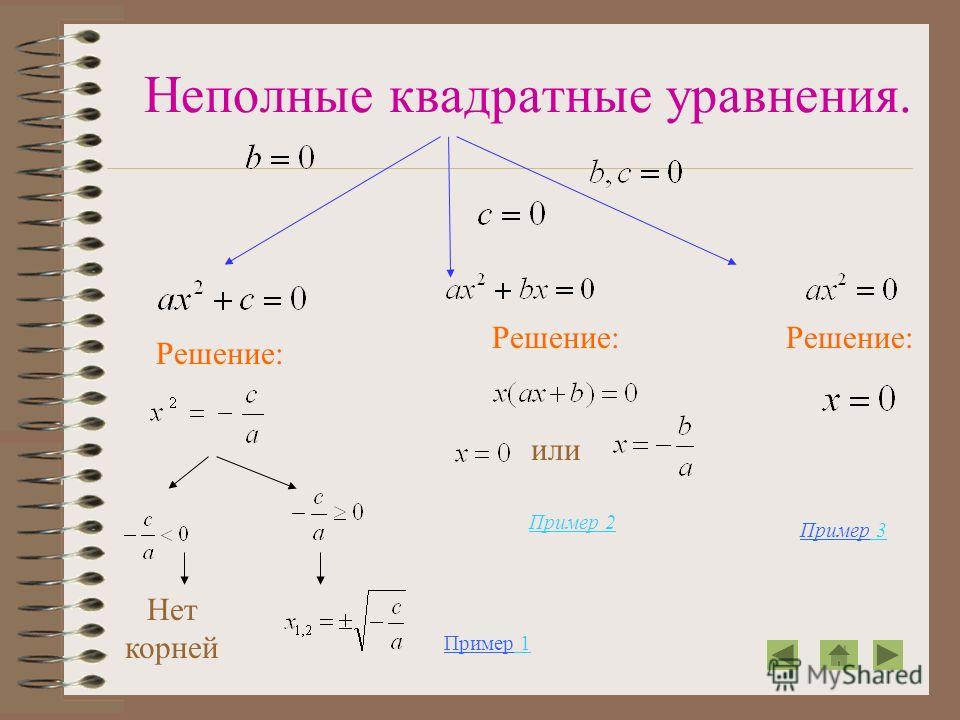
Неполные квадратные уравнения
Квадратные уравнения могут иметь отличия от определений. К примеру:
- x2 + 9x = 0;
- x2 − 16 = 0.
Видно, что в уравнениях нет одного слагаемого. Эти квадратные уравнения вычисляются намного легче, чем уравнения стандартного плана, потому что тут не нужно считать дискриминант.
Разберем положение:
Неполное квадратное уравнение: ax2 + bx + c = 0,
где b = 0 или c = 0, то есть коэффициент или свободный элемент = 0 при переменной x.
Или в более сложном случае b = c = 0, где оба коэффициента = 0.
И тогда уравнение уже выглядит так: ax2 = 0.
И у него единственный корень: x = 0.
Также следует изучить и другие способы:
Например: b = 0, и мы здесь получаем неполное квадратное уравнение: ax2 + c = 0.
Если чуть-чуть его преобразовать, то получится:
Решение неполного квадратного уравнения
Из-за того, что квадратный корень получается лишь из неотрицательного числа, то крайнее равенство имеет смысл только при (−c/a) ≥ 0.
На основании чего делаем заключение:
1) Когда в неполном квадратном уравнении: ax2 + c = 0
есть неравенство (−c/a) ≥ 0, то получится два корня.
2) А когда (−c/a)< 0, то корней не будет.
Таким образом дискриминант нам даже не потребовался. В неполных квадратных уравнениях трудных вычислений нет.
Поэтому не нужно помнить неравенство (−c/a) ≥ 0. Можно указать величину x2 и взглянуть, что находится с противоположной стороны от знака (=) равно.
Если какое-то положительное число — то в нем будет два корня.
Если какое-то отрицательное число — то корней здесь вообще не будет.
Далее необходимо разобраться с уравнением: ax2 + bx = 0,
Здесь свободный элемент = 0. А значит будет всегда именно 2 корня.
Нужно только многочлен распределить на множители:
Если какой-то множитель = 0, то произведение тоже будет = 0.
Вычисление квадратных уравнений:
- x2 − 7x = 0;
- 5×2 + 30 = 0;
- 4×2 − 9 = 0.
x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.
5×2 + 30 = 0 ⇒ 5×2 = −30 ⇒ x2 = −6.
Корни здесь отсутствуют, поскольку квадрат не является отрицательному числу равным.
4×2 − 9 = 0 ⇒ 4×2 = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.
Пример решения с помощью дополнения до полного квадрата
Приведем пример уравнения квадратного для тренировки его решения методом изложенным в предыдущем пункте. Пусть дано уравнение квадратное -10 — 6*x+5*x2 = 0. Начинаем решать его, следуя описанному выше алгоритму.
Пункт 1. Используем метод переброски при решении уравнений квадратных, получаем: — 6*x+5*x2 = 10.
Пункт 2. Приведенный вид этого уравнения получается путем деления на число 5 каждого его члена (если равенства обе части поделить или умножить на одинаковое число, то равенство сохранится). В результате преобразований получим: x2 — 6/5*x = 2.
Пункт 3. Половина от коэффициента — 6/5 равна -6/10 = -3/5, используем это число для составления полного квадрата, получаем: (-3/5+x)2. Раскроем его и полученный свободный член следует вычесть из части равенства левой, чтобы удовлетворить исходному виду квадратного уравнения, что эквивалентно его добавлению в правую часть. В итоге получаем: (-3/5+x)2 = 59/25.
Пункт 4. Вычисляем квадратный корень с положительным и отрицательным знаками и находим корни: x = 3/5±√59/5 = (3±√59)/5. Два найденных корня имеют значения: x1 = (√59+3)/5 и x1 = (3-√59)/5.
Поскольку проведенные вычисления связаны с корнями, то велика вероятность допустить ошибку. Поэтому рекомендуется проверить правильность корней x2 и x1. Получаем для x1: 5*((3+√59)/5)2-6*(3+√59)/5 — 10 = (9+59+6*√59)/5 — 18/5 — 6*√59/5-10 = 68/5-68/5 = 0. Подставляем теперь x2: 5*((3-√59)/5)2-6*(3-√59)/5 — 10 = (9+59-6*√59)/5 — 18/5 + 6*√59/5-10 = 68/5-68/5 = 0.
Таким образом, мы показали, что найденные корни уравнения являются истинными.
Решение интегралов
Онлайн калькулятор предоставляет инструменты для интегрирования функций. Вычисления производятся как с неопределенными, так и с определенными интегралами. Ввод интегралов в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:∫ f(x) — для неопределенного интеграла;ba∫ f(x) — для определенного интеграла.
В определенном интеграле кроме самой функции необходимо задать нижний и верхний пределы.
Примеры вычислений интегралов:
$$\int \left(\frac{x^4}{x^3-6x^2+11x-6}\right)dx$$ (найти интеграл функции)
$$\int \left(\sqrt{x\sqrt{x\sqrt{x}}}\right)dx$$ (решить интеграл)
$$\int \left(\left(x^2+3x+5\right)\cos 2x\right)dx$$ (вычислить интеграл)
$$\int \left(\frac{x+\arccos ^2\left(3x\right)}{\sqrt{1-9x^2}}\right)dx$$ (решить интеграл)
$$\int _1^{e^3}\left(\frac{1}{x\sqrt{1+\log \left(x\right)}}\right)dx$$ (найти интеграл функции)
$$\int _{\frac{\pi }{6}}^{\frac{\pi }{3}}\left(\sin 6x\sin 7x\right)dx$$ (решить интеграл)
$$\int _{+\infty }^{-\infty }\left(\frac{1}{\left(x^2+1\right)\left(x^2+4\right)}\right)dx$$ (решить интеграл)
$$\int _1^2\left(x^2+\frac{1}{x}+\frac{1}{x^3}\right)dx$$ (вычислить интеграл)
Решение уравнений и неравенств
Математический калькулятор может решать уравнения и неравентства относительно переменной «x». Если есть необходимость найти другую переменную, например «y», то следует просто поменять их местами в выражении. Ввод переменных «x»,»y»,»z» производится в группе xyz нажатием соответствующих кнопок x, y, z.
Примеры решений уравнений и неравенств:
$$\frac{5}{12}+\frac{x}{6}=\frac{x}{4}+\frac{1}{3}$$ (решить уравнение)
$$x^2+12x+36=0$$ (решить уравнение)
$$\left(x+8\right)^2=x^2+8$$ (решить уравнение)
$$\left(x^2+\frac{1}{x^2}\right)+\left(x+\frac{1}{x}\right)=4$$ (решить уравнение)
$$\frac{19-x^2-4x}{49-x^2}(решить неравенство)
$$\frac{x}{3}+\frac{2x-1}{5}>2x-\frac{1}{15}$$ (решить неравенство)
$$\frac{\left(x-1\right)^2\left(x+7\right)\left(x+3\right)^3}{x^2+6x+9}\ge 0$$ (решить неравенство)
Примеры
Пишем в поле ввода коэффициенты
4 8-i -i
Не забудьте, что как минимум одним пробелом разделяются эти значения
ответ будет следующий
| Вы ввели следующее выражение |
| Результат решения заданного уравнения |
|
Решаем комплексное уравнение: x^2 + (2-0.25i)*x + (0-0.25i)= 0 |
Давайте проверим, а правильно ли нам посчитал бот эти корни. Для этого воспользуемся Аргумент и значения функции комплексной переменной и посчитаем чему же будет равно значение функции, при полученных корнях
При выборе первого корня ответ будет такой:
| Вы ввели следующую функицю | ||||
| Табличное представление значений функции | ||||
|
Несмотря на небольшую погрешность, результат говорит нам о том что расчеты проведены верно
Здесь мы видим, что коэффициенты представлены в виде комплексных выражений, но для бота это не помеха.
пишем в запросе
2-i ln(1+sin(i)) -3
и получаем результат
| Вы ввели следующее выражение |
 |
| Результат решения заданного уравнения |
|
Решаем комплексное уравнение: x^2 + (0.0003584355453+0.4330639593925i)*x + (-1.2-0.6i)= 0 |
Удачи в расчетах!
- Квадратные сравнения. Нормирование >>
Как решить квадратные уравнения онлайн
Что такое квадратное уравнение и почему оно так называется? Основой данного расчета будет график квадратичной функции, где необходимо рассчитать точку Х – корень данной формулы.
Решение (корень) – это координаты пересечения параболы с Х-осью (абцисс). Парабола считается квадратичной функцией, если она не имеет общего соприкосновения с данной осью, то можно сказать: в этом уравнении корни отсутствуют.
Если наблюдается одно пересечение параболы и оси абцисс – на вершине фигуры параболы, здесь будет один-единственный корень, его возможно вычислить (либо принято говорить, что здесь имеется два идентичных корня).
Когда парабола встречается с Х-осью в двух местах, то здесь можно рассчитать два корня (вещественных).
Роль в расчетах играет коэффициент а. Если он плюсовой, то «ветви» параболы идут в верхнюю секцию графика, вдоль оси Х. Если в минусе – все наоборот. Также используется коэффициент b. Он отвечает за положение параболы по отношению к оси Y. Если коэффициент b – плюсовой, то вершина фигуры находится слева, при отрицательном значении вершина размещена в правой .
Перед вами формула для правильного вычисления: ax2+bx+c=0
- Необходимо переставить С вправо: ax2+bx=-c
- Перемножить все уравнение на переменную а: (2ax)2+4abx=-4ac
- Затем перемножить всю сторону на 4а.
- Добавить b2 к обеим частям уравнения: (2ax)2+4abx+b2= b2-4ac
- Слева выделить из действия полный квадрат: (2ax+b)2= b2-4ac
- Затем извлекаем квадратный корень: 2ax+b=±√b2-4ac
- Теперь переносим b вправо: 2ax=-b±√b2-4ac
- Поделим все уравнение на 2а и получим готовый корень:
x=-b ±√b2 – 4ac / 2a
Если вы чувствуете неуверенность при освоении алгебры, программа кажется сложной – не отчаивайтесь. Онлайн-калькулятор всегда выручит – при подготовке домашнего задания, контрольной, зачета, проверочной или лабораторной. Удобно использовать расчеты по формулам, которые недоступны на обычном счетном инструменте. Здесь не может быть ошибок, а небольшая практика облегчит понимание любой темы. Прорешайте буквально два-три упражнения, и вы скоро поймете логику процесса.
Упрощение выражений, раскрытие скобок, разложение многочленов на множители
Калькулятор позволяет произвести некоторые алгебраические преобразования с выражениями. Результат выводится в нескольких вариантах упрощения/разложения/раскрытия скобок и пр.
Примеры:
$$x^4+x^2a^2+a^4$$ (разложить на множители)
$$\frac{6x^3-24x^2}{6x^3}$$ (разложить на множители)
$$(5x-2y^2)(5x+2y^2)$$ (раскрыть скобки)
$$(a-b)(a+b)(a^2+b^2)(a^4+b^4)(a^8+b^8)$$ (раскрыть скобки)
$$\frac{a^3-8}{a^2+2a+4}$$ (раскрыть скобки)
$$\frac{\left(\frac{2a}{2a+b}-\frac{4a^2}{4a^2+4ab+b^2}\right)}{\left(\frac{2a}{4a^2-b^2}+\frac{1}{b-2a}\right)}+\frac{8a^2}{2a+b}$$ (упростить выражение)
$$\frac{1-\sin ^4\left(x\right)-\cos ^4\left(x\right)}{2\sin ^4\left(x\right)}+1$$ (упростить выражение)
$$\left(\sqrt{a}-\frac{a}{\sqrt{a}+1}\right)\cdot \frac{a-1}{\sqrt{a}}$$ (упростить выражение)
SnapCalc — решение примеров и уравнений
Приложение, которая займется математикой вместо вас или поможет сверить ответы. В отличии от предыдущих его минус, что оно платное и на английском. Но даже кто не знает язык — сможет разобраться. Итак, для начала скачиваем приложение. подойдет как для андроид, так и айфона.
Нам дают 3 пробных бесплатных дня, после чего оплата составляет 2350 рублей за 3 месяца. Итого, 783 рубля в месяц. Но мы можем только воспользоваться пробным периодом и сразу же отписаться, это вас ни к чему не обязывает. Просто потом в настройках перейдете в подписку, увидите нужное приложение и кликните «Отменить пробную подписку». Даже если в первый день отменить, потом можно пользоваться эти три дня.
Далее можем пользоваться, принцип действие похож на предыдущее. Открывается камера с формой, куда нужно поместить пример. После чего делаем фото и получаем ответ. Также потом можно посмотреть последовательность, что и как было сделано.
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
- ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax 2 + c = 0, при b = 0;
- ax 2 + bx = 0, при c = 0.
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.
Как решить уравнение ax 2 = 0
Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.
Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.
Пример 1. Решить −6x 2 = 0.
- Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
Как решить уравнение ax 2 + с = 0
Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
- перенесем c в правую часть: ax 2 = — c,
- разделим обе части на a: x 2 = — c/а.
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.
| В двух словах |
|---|
Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:
не имеет корней при — c/а 0.
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
- Перенесем свободный член в правую часть:
Разделим обе части на 8:
В правой части осталось число со знаком минус, значит у данного уравнения нет корней.
Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.
Как решить уравнение ax 2 + bx = 0
Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:
Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:
Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0
Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
Решить линейное уравнение:
0,5x = 0,125, х = 0,125/0,5
Значит корни исходного уравнения — 0 и 0,25.
Ответ: х = 0 и х = 0,25.
Как разложить квадратное уравнение
С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:
Формула разложения квадратного трехчлена
Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2).
Действия над комплексными числами
Онлайн калькулятор имеет функционал для работы с комплексными числами (операции сложения, вычитания, умножения, деления, возведения в степень и пр.). Комплексное число обзначается символом «i» и вводится с помощью групповой кнопки xyz и кнопки i
Примеры операций с комплексными числами:
$$\frac{\left(1+i\right)\left(3+i\right)}{3-i}-\frac{\left(1-i\right)\left(3-i\right)}{3+i}$$ (найти разность комплексных чисел)
$$\left(1-i\right)^3+\left(1+i\right)^3$$ (найти сумму комплексных чисел)
$$\left(-2+3i\right)\left(5+4i\right)$$ (найти произведение комплексных чисел)
$$\frac{-5-6i}{-6i}$$ (найти частное комплексных чисел)
$$\left(-2+2i\right)^9$$ (выполнить возведение комплексного числа в степень)
$$\frac{\left(-7-8i\right)i^7}{\left(4-5i\right)\left(-3+i\right)}-\frac{4+4i}{-2-5i}$$ (выполнить действия над комплексными числами)
Важность квадратного уравнения в реальной жизни:
Будучи студентом, вас могут принимать во внимание по различным вопросам математики. Кроме того, студенты обычно используют это уравнение в таких предметах, как решать квадратные уравнения инженерия и физика
Есть и другие профессии, которые используют (квадратные уравнения):
- Военные и правоохранительные органы – (для определения траектории ракет, выпущенных артиллерией)
- Инженеры – (относится к гражданскому строительству)
- Уравнение движения (как на игровой площадке, так и в игровых ситуациях, оно описывает траекторию полета мяча и определяет высоту брошенного мяча)
- Наука (Астрономы – описывают орбиту планет, солнечных систем и галактик)
- Сферы сельского хозяйства (оптимальное расположение границ для производства самого большого поля)
Метод определения корней
Чтобы вычислить то, сколько имеется корней в уравнении, следует воспользоваться дискриминантом.
Дискриминант
У уравнения a·x2 + b·x + c = 0 дискриминант является обычным: D = b2 − 4ac.
Представленную формулу желательно хорошенько выучить
Совершенно не важно ее происхождение. Основным является то, сколько именно корней будет находиться в квадратном уравнении
Это определяется по дискриминанту.
Делается все следующим образом:
- Если D < 0, корней нет;
- Если D = 0, есть только один корень;
- Если D > 0, будет два корня.
Очень важно учесть то, что дискриминант всегда говорит о том, сколько корней, а не обозначений. Если обратиться к примерам, то все станет понятным:
Если обратиться к примерам, то все станет понятным:
Возьмем задачу именно на количество корней, имеющих квадратные уравнения:
- x2 − 8x + 12 = 0;
- 5×2 + 3x + 7 = 0;
- x2 − 6x + 9 = 0.
После чего запишем коэффициенты для 1-го уравнения и таким образом, определим дискриминант:
- a = 1, b = −8, c = 12;
- D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
В итоге мы получаем положительный дискриминант. Именно поэтому уравнение будет содержать два разных корня.
У другого уравнения решение точно такое же:
- a = 5; b = 3; c = 7;
- D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Здесь корней нет, а дискриминант отрицательный.
Сделаем еще один разбор:
- a = 1; b = −6; c = 9;
- D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Итог: Один корень, дискриминант равняется 0.
Также очень важно, чтобы коэффициенты были написаны к конкретному уравнению. Возможно это нудно и долго — но зато есть гарантия того, что никакие глупые ошибки не произойдут, а коэффициенты не перепутаются
И здесь нужно самостоятельно сделать ставку либо на скорость, либо на качество.
Если выработать определенную сноровку, то через какое-то время выписывать коэффициенты совсем не потребуется. Все эти манипуляции и вычисления будут спокойно выполняться в уме. Это будет происходить у большинства людей примерно после того, как будет решено около 70-ти уравнений. Согласитесь, что цифра не такая уж значительная.
Корни квадратного уравнения
Важнейшая формула корня квадратного уравнения при дискриминанте D > 0
Если D = 0, то, пользуясь такими формулами, можно получить такое же число. Именно оно и будет являться ответом.
А если, например, D < 0 и корней нет, то считать больше не нужно.
Таким образом, когда есть знание формул и умение считать, то никаких проблем не будет. Обычно разного рода накладки могут появляться, когда в формулу подставляются отрицательные коэффициенты.
На помощь придет прием, когда нужно глядя на формулу перед собой, конкретно расписывать свои действия. Тогда можно быстро устранить все ошибки.
Пример использования теоремы Виета
Необходимо составить квадратное уравнение, если известно, что оно имеет вид x2+c = -b*x и корни его равны 3 и -4.
Поскольку в рассматриваемом уравнении a=1, то формулы Виета будут иметь вид: x2+x1 =-b и x2*x1= с. Подставляя известные значения корней, получаем: b = 1 и c = -12. В итоге восстановленное уравнение квадратное приведенное будет вид иметь: x2-12 = -1*x. Можно подставить в него значение корней и убедиться, что равенство выполняется.
Обратное применение Виета теоремы, то есть вычисление корней по известному виду уравнения, позволяет для небольших целых чисел a, b и c быстро (интуитивно) находить решения.
Как найти дискриминант
С помощью калькулятора онлайн можно узнать дискриминант, необходимый для операций с квадратичными уравнениями. Для расчета D нужно определить число, равное: D=b2−4ac.
Если тут есть вещественные коэффициенты и от нуля до пары корней, то они зависят от дискриминирующего показателя:
Если D>0, то будет два варианта ответа, которые вычисляются по такой схеме:
x1,2= -b ± √D / 2a
Если D меньше нуля, то корней нет, есть только два решения, найти их можно через следущие шаги:
x1,2 = -b ± i√-D / 2a
Если D равняется нулю, то имеет место единственный корень или пара совпадающих, кратные 2.
Итак, вы научились находить дискриминант – половина решения уже, можно сказать, в кармане. Остальные математические действия уже в кармане, просто дорешайте пример по алгоритму. И все задания будут выполнены на «отлично»!
Задания для самостоятельного решения
Задание 1. Решить уравнение:
Решение:
Ответ: 2; −2.
Задание 2. Решить уравнение:
Решение:
Ответ: корней нет.
Задание 3. Решить уравнение:
Решение:
Ответ: 3; −3.
Задание 4. Решить уравнение, используя выделение полного квадрата:
Решение:
Ответ: 3; −13.
Задание 5. Решить уравнение, используя выделение полного квадрата:
Решение:
Ответ: 12; 4.
Задание 6. Решить уравнение, используя выделение полного квадрата:
Решение:
Ответ: 7; 5.
Задание 7. Решить уравнение:
Решение:
Ответ: 0; 1.
Задание 8. Решить уравнение:
Решение:
Ответ: 0; −3.
Задание 9. Решить уравнение:
Решение:
Ответ: 7; −7.
Задание 10. Решить уравнение:
Решение:
Ответ:
Задание 11. Решить уравнение:
Решение:
Ответ: 5; −5.
Задание 12. Решить уравнение:
Решение:
Ответ: 7; 2
Задание 13. Решить уравнение:
Решение:
Ответ: корней нет.
Задание 14. Решить уравнение:
Решение:
Ответ:
Задание 15. Решить уравнение:
Решение:
Ответ: 1; −5.
Задание 16. Решить уравнение:
Решение:
Ответ: 5; −9.
Задание 17. Решить уравнение:
Решение:
Ответ: −3; −4.
Задание 18. Решить уравнение:
Решение:
Ответ: .
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
В чем плюсы таких сервисов?
Вы можете подумать, что в ваше время такого не было и все сами решали и думали. Какая-то доля правды. Но такой функционал может пригодится родителям и учителям. Так как не всегда есть время вникать, что и как решить у детей, легче сверить, правильно ли он сделал и все. Ну и не все из нас математики, есть же ещё гуманитарный склад ума. Такие ученики могут быть отличниками на русском языке, гениально писать сочинения, но совсем не совладать с логарифмами и уравнениями. И в этом нет ничего плохого. Когда он вырастет, то пойдет в свою отрасль работать. Навряд-ли, ему захочется стать кандидатом математических наук. Так что взгляните на это под разными углами и, возможно, вам это не покажется преступлением.
Итак, обобщая:
- Не всем обязательно знать математику на 5 баллов. Главное, чтобы человек умел деньги считать и использовал свои сильные стороны;
- Помогает взрослым не тратить много времени, которого у них чаще всего нет.
- Может быть помощников для проверки себя на контрольной, так сказать, проверке своих знаний.
- Ну и учить все равно придется. Ведь, когда вас вызовут к доске — телефон не достанешь однозначно.
Что умеет данный калькулятор
Интернет-калькулятор – отличная находка для всех, кто хочет сэкономить учебные часы и силы на выполнение упражнений по алгебре. С этой программой легче моментально высчитать любой квадратичный корень, без сложностей, риска плохой оценки за домашнюю работу или контрольную.
Кроме ответа для задания, пользователь получает детальное, пошаговую разборку всего решения примера. Этот подход поможет быстро понять алгоритм и принципы всех математических действий. Будет основа понимания – как строить решение, корректно искать корень.
Такой метод помогает быстрее освоить учебную программу по алгебре, справиться со сложными заданиями, подтянуть успеваемость. Станет понятным даже новый и непонятный материал прошедшего урока. Почему бы не использовать такой удобный ресурс? Многое зависит также от ответственности и активности учащихся, как они воспользуются этой возможностью. Теперь любое, самое сложное квадратное уравнение онлайн покорится силе ума!
Теорема Виета
Вывести математическое доказательство этой формулы также выполняется посредством квадратичных вычислений, показанных на примере ниже.
Перед нами уравнение, где ведущий коэффициент x2=1. Получить эти данные можно, поделив полное выражение на а: x2+px+q=0, где p=ba, q=ca.
Получим сумму всех корней: x2+px+q=0. Она будет равна p, используемому с обратным значением. При этом произведение корней будет равно значению свободного члена q: x1+x2=-p, x1x2=q.
Это несложная теорема, которая, однако, важна для освоения школьной программы. Не смущайтесь, если что-то вначале непонятно. Всегда поможет наш сервис, который не ошибается в расчетах!
Как вычислить корни квадратного уравнения
Если любое уравнение – это рассчитанное тождество, где нужно определить одну или сразу несколько переменных, то что делать, если формула неполная? Есть решения и в этом случае. Тут также выручит калькулятор онлайн для квадратичных расчетов.
Следует вычислить неизвестные таким путем, чтобы в случае вставки в формулу получалось корректное равенство, проверка покажет правильность ответа.
Часто используются степени уравнения, они определяют по самой большой в формуле с неизвестным. Например, если неизвестный показатель находится в квадрате, то уравнение, соответственно, квадратное.
Классическое квадратное уравнение выглядит вот так: ax²+bx+c=0
Расшифруем значения переменных:
- а – старший коэффициент, он не может быть равен 0;
- b — следующий по значимости коэффициент;
- с – свободный член-переменная.
В первую очередь нужно вычислить количество возможных корней в данном расчете. Для этого смотрят на наличие дискриминанта. Он рассчитывается по простой формуле: D=b²−4ac. И у него есть свои математические свойства, которые нужно учитывать при вычислении корней:
- D<0 – корней нет;
- D=0 – есть один корень;
- D>0 – есть два различных корня
