Самое большое число
Из школьного курса известно, что наибольшего числа не существует. Ведь если к самому большому числу прибавить хотя бы единицу, то получим еще большее число. Школьник с легкостью скажет, что, например, самое большое двузначное число — 99, а трехзначное — 999 и т.д.
Существует два алгоритма наименования чисел – английский и американский.
В американском названия больших чисел строятся следующим образом: сначала идет латинское порядковое числительное, а затем добавляется суффикс «иллион». Исключение – миллион. Далее получаются числа: триллион, квадриллион, квинтиллион. После идут секстиллион, септиллион, октиллион, нониллион и дециллион. Такой способ используют в США, Канаде, России и Франции.
![]() Американский алгоритм наименования чисел
Американский алгоритм наименования чисел
Английский алгоритм используют в Испании и Великобритании, а так же в ряде бывших колоний.
Здесь названия строятся так: к латинскому числительному прибавляют суффикс «иллион», к следующему числу (которое больше в 1000 раз) уже добавляют суффикс «иллиард».
После триллиона идет триллиард, после квадриллион, квадриллиард и т.д. Получается, что по английскому и американскому алгоритму одни и те же большие числа называются по-разному.
Читайте по теме: Самое маленькое число
В русский язык из английской системы пришел только миллиард (109), который американцы называют биллионом. Иногда в России употребляют слово триллиард, т.е. 1000 триллионов или квадриллион.
Самое большое простое число в мире – 274207281 – 1, которое содержит 22 338 618 десятичных цифр (простое число Мерсенна). Значение нашли в 2015 году в ходе проекта по распределенному поиску простых чисел Мерсенна GIMPS.
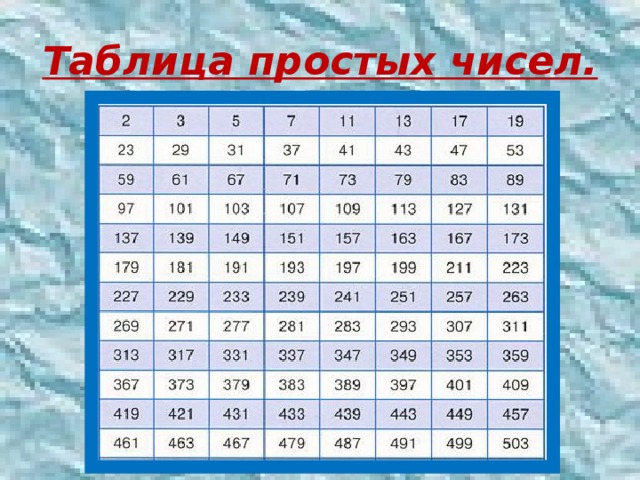
Поясним, что простыми называются натуральные (целые положительные) числа, имеющие только два делителя — единицу и само себя. Например, 2, 3, 5, 7 — простые числа. Список продолжают 11, 13, 17, 19… Кроме двойки все числа нечетные, иначе бы делились не только на единицу и себя, но и на два.
Значит, найденное простое число еще и самое большое из нечетных.
![]() Маренн Марсен и самое большое простое число
Маренн Марсен и самое большое простое число
По утверждению Евклида, простых чисел бесконечное множество, значит, наибольшего простого числа нет. Ученые до сих пор ищут числа-рекордсмены. И тому есть разумное объяснение. Всемирная организация Electronic Frontier Foundation учредила награды за подобные открытия: чем больше найденное число, тем выше награда.
Есть специальный способ проверки простоты чисел, который называется тест Люка-Лемера. Правда, предназначен он исключительно для чисел Мерсенна. Что же это за числа? Это вид натуральных чисел, расположенных в определенной последовательности. Имя им дал французский математик Мерсенн Марен. Вид числа Мерсенна такой:
Mn = 2n – 1,
где n — натуральное число.
При n = 1, 2, 3, 4, … числа Мерсенна образуют последовательность, начинающуюся с 1, 3, 7, 15. Затем идут 31, 63, 127. Продолжают ряд 255, 511, 1023, 2047 и т.д.
Такие числа используют в криптографии, например, для усовершенствования банковских кодов.
Внесистемные числа
Кроме чисел, которые записаны при помощи английской или американской систем, известны внесистемные числа. У них есть собственные названия, в которых нет латинских префиксов. Для понимания сначала рассмотрим запись латинскими числительными.
Единица – это 100, десять — 101 и так далее: миллиард — 109, триллион — 1012, квадриллион — 1015, квинтиллион — 1018, секстиллион — 1021, септиллион — 1024, октиллион — 1027, нониллион — 1030, дециллион — 1033.
С помощью приставок можно и дальше выводить числа: андециллион, дуодециллион, тридециллион и так далее. Но нужны собственные названия чисел, а тут только составные названия. Поэтому по этой системе собственных имен еще только три — вигинтиллион — 1063, центиллион — 10303, миллеиллион — 103003.
![]() В миллеиллионе 3003 нуля
В миллеиллионе 3003 нуля
Число с собственным, а не составным названием больше 103003 получить невозможно. Однако числа больше миллеиллиона известны – это внесистемные числа.
Самое маленькое внесистемное число носит название мириада. Означает сотню сотен, т.е. 10000.
Какое самое большое число в мире
В 1980 году в Книгу рекордов Гиннеса вошло число Грэма (оно же G64 или G), названное в честь американского математика Рональда Грэма
Оно является наибольшим числом, которое когда-либо использовалось в важном математическом доказательстве. Речь идет про теорию Франка Рамсея
Кратко об этой теории: представим себе N-мерный куб, его вершины в случайном порядке соединены красными или синими отрезками-линиями. А наша задача — понять, до какого значения N возможно (если по-разному закрашивать ребра куба), избежать ситуации, при которой одна плоскость в кубе будет окрашена одним цветом. То есть у нас не должен получиться одноцветный «конвертик».
![]()
Математики позакрашивали кубик и так и эдак, получилось, что до шестимерного куба можно исхитриться и сделать, чтобы линии одного цвета, соединяющие четыре вершины, не лежали в одной плоскости. А вот с семимерным, как выяснили Грэм и Ротшильд, такой фокус уже не провернешь. И с восьмимерным. И… «и так далее», которое, впрочем, не бесконечно, а заканчивается фантастически гигантским числом. Вот его-то и именуют числом Грэма. Кстати, в настоящее время решение Грэма и Ротшильда устарело. Математики выяснили, что 6-7-8-9-10-11-12-мерные кубы все же можно покрасить без «конвертов». Но где-то в промежутке между 13 и числом Грэма гарантированно есть число выше которого «конверты» в любом случае будут.
Число Грэма получило всемирное признание в 1977 году, когда известный популяризатор науки Мартин Гарднер написал об этом в Scientific American.
И хотя с тех пор в математической науке были и другие кандидаты на титул самого большого числа, «детище» Грэма является самым распиаренным и общеизвестным. И если вы слышали про «гугольное семейство»:
- гугол — 10100; Или: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
- гуголплекс — 10гугол,
то знайте, что этими числами в математике лишь «разминаются», а число Грэма в немыслимое количество раз больше, чем они. И даже больше, чем число Скьюза, находящееся между 1019 и 1,3971672·10316 и приблизительно равное e727,951336108.
Любопытно, что придумав гугол американский математик Эдвард Казнер хотел показать студентам разницу между невероятно большим числом и бесконечностью. Тогда число Грэма может просто «взорвать мозг».
Досчитаем до дециллиона
Давайте посчитаем еще. Например, спичечный коробок, увеличенный в тысячу раз, будет размером с шестнадцатиэтажный дом. Увеличение в миллион раз даст «коробок», который по площади больше Санкт-Петербурга. Увеличенный в миллиард раз, коробок не поместится на нашей планете. Наоборот, Земля поместится в такой «коробок» 25 раз!
Если считать дальше, то масштабы Земли окажутся уже недостаточными. Увеличенный в триллион раз коробок мог бы вместить в себя все планеты Солнечной системы вместе с их спутниками, а также астероиды и кометы. В коробке, который увеличен в квадриллион раз, Солнечная система могла бы поместиться полностью.
Увеличение коробка дает увеличение его объема. Вообразить себе такие объемы при дальнейшем увеличении будет уже почти невозможно. Для простоты восприятия попробуем увеличивать не сам предмет, а его количество, и расположим спичечные коробки в пространстве. Так будет легче ориентироваться. Квинтиллион коробков выложенных в один ряд, протянулись бы дальше звезды α Центавра на 9 триллионов километров.
Еще одно тысячекратное увеличение (секстиллион) позволит спичечным коробкам, выстроенным в линию, перегородить всю нашу галактику Млечный путь в поперечном направлении. Септиллион спичечных коробков растянулись бы на 50 квинтиллионов километров. Такое расстояние свет сможет пролететь за 5 миллионов 260 тысяч лет. А выложенные в два ряда коробки протянулись бы до галактики Андромеды.
Осталось только три числа: октиллион, нониллион и дециллион. Придется напрячь воображение. Октиллион коробков образует непрерывную линию в 50 секстиллионов километров. Это боле пяти миллиардов световых лет. Не каждый телескоп, установленный на одном краю такого объекта, мог бы разглядеть его противоположный край.
Считаем дальше? Нониллион спичечных коробков заполнил бы собой все пространство известной человечеству части Вселенной со средней плотностью 6 штук на кубический метр. По земным меркам вроде бы не очень-то и много – 36 спичечных коробков в кузове стандартной «Газели». Но нониллион спичечных коробков будет иметь массу в миллиарды раз больше чем масса всех материальных объектов известной Вселенной вместе взятых.
Дециллион. Величину, а скорее даже величественность этого исполина из мира чисел трудно себе вообразить. Только один пример – шесть дециллионов коробков уже не поместились бы во всей доступной человечеству для наблюдения части Вселенной.
Еще более поразительно величественность этого числа видна, если не умножать количество коробков, а увеличить сам предмет. Спичечный коробок, увеличенный в дециллион раз, вместил бы в себя всю известную человечеству часть Вселенной 20 триллионов раз. Невозможно такое себе даже просто представить.
Небольшие подсчеты показали, насколько огромны числа, известные человечеству уже несколько веков. В современной математике известны числа во много раз превосходящие дециллион, но применяются они только в сложных математических вычислениях. Сталкиваться с подобными числами приходится только профессиональным математикам.
Самым известным (и самым маленьким) из таких чисел является гугол, обозначаемый единицей со ста нулями. Гугол больше чем общее число элементарных частиц в видимой нам части Вселенной. Это делает гугол абстрактным числом, которое не имеет большого практического применения.
Краткая история[править | править код]
Термин «миллион» итальянского происхождения и встречается уже в первой печатной арифметике (анонимной), вышедшей в итальянском городе Тревизо в 1478 году, и ещё ранее в нематематической книге путешественника Марко Поло (умер в 1324 году), а в форме «миллио» еще раньше — в рукописи 1250 года.
В рукописи французского математика XV века Никола Шюке впервые появляются термины «биллион» — 1012, «триллион» — 1018 и дальнейшие; в печатном руководстве биллион в значении 1012 появляется в 1602 году.
В XVII веке во Франции начали употреблять короткую шкалу: «биллион» — 109, «триллион» — 1012 и т. д.
Слово «миллиард», имевшее вначале значение 1012, получило значение 109 (тысячи миллионов) в «Арифметике» Траншана (1558) и употреблялось во Франции в XIX веке наравне со словом «биллион». В Германии это слово вошло в употребление лишь после получения от Франции 5 миллиардов контрибуции после франко-прусской войны 1871 года.
Для чтения чисел с большим количеством цифр анонимная рукопись 1200 года впервые рекомендует разбить цифры на группы по 3 или отмечать группы точками вверху или дугами; это же затем рекомендует Леонардо Пизанский (1228). К этой системе приходят и последующие авторы, однако они не предлагали названий. Введённые Шюке наименования больших чисел, но с группировкой цифр по 6 относятся к системе наименования чисел с длинной шкалой.
Использование систем наименования чисел в мире:
| короткая шкала длинная шкала | обе шкалы другие системы |
В России первоначально была введена система наименования чисел с длинной шкалой, и, по-видимому, в печатном виде впервые в 1703 году в «Арифметике» Л. Ф. Магницкого. Однако в конце XVIII века, в царствование императора Павла I, вслед за Францией произошёл переход на короткую шкалу. Так, в опубликованном в 1798 году переводе части первой — «Арифметика» — «Курса математики» Этьенна Безу введена система наименования чисел с короткой шкалой, при том, что в опубликованной в 1791 году книге «Арифметика или числовник» Н. Г. Курганова (1725 или 1726—1796) используется длинная шкала. Длинная шкала встречается и в некоторых русских учебниках XIX века, однако к XX веку фактически закрепилась короткая шкала.
В 1948 году IX Генеральная конференция по мерам и весам приняла предложение Международного комитета мер и весов, рекомендующего для европейских стран применение длинной шкалы. Франция вернулась к системе с длинной шкалой, а в России продолжалось использование системы с короткой шкалой, которая была заимствована во Франции ранее. Однако, использование длинной шкалы предусматривается рекомендацией Совета экономической взаимопомощи PC 2625—70 «Основные математические обозначения», где приводятся основные математические обозначения, употребляемые в нормативно-технической документации, научной и технической литературе и в школьных учебниках. Последнее позволяет утверждать, что официально во всех странах, образовавшихся после распада СССР, с 1970 года действует именно длинная система наименований чисел, хотя фактически продолжает применяться короткая система.
В США короткая шкала используется с XIX века; Великобритания перешла на неё в 1974 году.
Внесистемные числа
Помимо чисел, которые записываются по известным системам (приведенным выше), существуют еще и внесистемные. Они обладают своими названиями, в которых не включаются латинские префиксы.
Начать их рассмотрение можно с числа, называемого мириадой. Определяется оно как сотня сотен (10000). Но по своему назначению это слово не применяется, а употребляется в качестве указания на бесчисленное множество. Даже словарь Даля любезно предоставит определение такого числа.
Следующим после мириады идет гугол, обозначающий 10 в степени 100. Впервые это наименование было употреблено в 1938 году – математиком из Америки Э.Каснером, отметившим, что это название придумал его племянник.
![]()
В честь гугола свое название получил Google (поисковая система). Затем 1-ца с гуголом нулей (1010100) представляет собой гуголплекс – такое название придумал тоже Каснер.
Еще большим по сравнению с гуголплексом является число Скьюза (е в степени е в степени е79), предложенное Скьюзом при доказательстве гипотезы Риммана о простых числах (1933 год). Есть и еще одно число Скьюза, но оно применяется, когда несправедлива гипотеза Риммана. Какое из них больше, сказать довольно сложно, особенно если речь заходит о больших степенях. Однако и это число, несмотря на свою «огромность», не может считаться самым-самым из всех тех, которые обладают своими названиями.
А лидером среди самых больших чисел в мире является число Грэма (G64). Именно его использовали в первый раз для проведения доказательств в области математической науки (1977 год).
![]()
Когда речь идет о таком числе, то нужно знать, что без специальной 64-уровневой системы, созданной Кнутом, не обойтись – причина тому связь числа G с бихроматическими гиперкубами. Кнутом была придумана сверхстепень, а для того чтобы было удобно делать ее записи, он предложил использование стрелок вверх. Вот мы и узнали, как называется самое большое число в мире. Стоит отметить, что это число G попало на страницы известной Книги рекордов.
Поверья и легенды
![]()
Но почему люди так предвзято относятся к нему, считая 13 сатанинским числом, не несущим ничего кроме проблем, неприятностей, несчастий?
Первые упоминания о несчастливой сущности числа 13 появились в весьма отдаленные от нас времена, когда у людей еще не было письменности, но потребность в подсчете различных предметов уже появилась. Цифры обозначались жестами, знаками, а для счета использовались пальцы на руках (10) и сами руки (еще 2 единицы). Итого, без проблем можно было вести счет до 12. А если элементов было 13? Столкнувшись с такой сложной проблемой люди стали избегать это «несчастливое» число при ведении подсчетов.
У христиан, согласно версии некоторых теологов, «нелюбовь» к этому числу объясняется событиями, связанными с Тайной Вечерей, на которой присутствовали 12 апостолов и сам Иисус Христос. Чем все закончилось, мы хорошо знаем! Иуда предал Божьего Сына!
Не менее печальная история есть и у жителей стран Скандинавии. В одной из легенд говорится об ужине, на котором присутствовали 12 верховных божеств, к которым в последний момент присоединился Локи, бог хитрости, обмана, коварства, лжи. Где бы он ни появлялся, там всегда происходят трагические события. Так было и в тот раз: погиб Бальдер, бог весны и света, покровитель воинов, чародей.
Но не все так однозначно. У некоторых народов число 13 вызывает исключительно положительные эмоции.
- Оно широко распространено на египетских фресках, изображающих фараонов, украшает гробницы, где выступает в качестве оберега, талисмана, амулета, обозначая благополучие, богатство. Древние Египтяне верили, что человек проходит жизненный путь, включающий 13 фаз. Последний этап предполагает посещение загробного мира. Чтобы умершему было там хорошо, его нужно проводить с радостью.
- Счастливым считалось это число и у народности майя, жившей на территории Южной Америки. Созданный ими календарь насчитывал в году 13 месяцев. Столько же было у них и знаков Зодиака. Кроме привычного нам набора созвездий, в зодиакальную систему входил еще и Змееносец. Именно этот календарь используется многими знаменитыми астрологами при выполнении расчетов наряду с другими ритуальными предметами. Заканчивался он 13 месяцем 2012 года. Это стало одной из основных причин паники о якобы надвигающемся «конце света». Однако на самом деле это свидетельствовало лишь о вхождении Земли в новую эру, что сопровождалось трансформацией мира. Выходом из эры падения (железного века демона Кали). Кстати согласно славянскому календарю мы входим в эру волка.
- В Китае и в Италии это число также считается счастливым. Оно символизирует плодородие, плодовитость, потенцию. То есть, по сути, речь также идет о трансформации, только не о конце жизненного пути, а о его начале. Жители этих стран считают удачей жить в доме (квартире) с номером 13. Небольшие сувениры, монеты с этим числом развешивают в разных местах дома, надеясь, что они привлекут в семью счастье, помогут гармонично настроить семейные отношения.
Примерно аналогичный смысл имеет число 13 и в Японии. Складывая цифры 1 и 3 в сумме получаем 4, что созвучно слову смерть на японском языке. Но и в данном случае это означает не конец, а переход в новую форму сущности.
Гуголплекс
Это число – производная от гугола, но ощутимо больше его. Приставка «плекс» означает, возведениее десятки в степень, равную основному числу, таким образом, гулоплекс – это 10 в степени 10 в степени 100 или 101000.
Получившееся число – превышает количество частиц в обозримой Вселенной, которое оценивается где-то в 1080 степени. Но это не помешало ученым увеличивать число простым добавлением к нему приставки «плекс»: гуголплексплекс, гуголплексплексплекс и так далее. А для особо извращенных математиков изобрели вариант увеличения без бесконечного повторения приставки «плекс» — перед ней просто ставят греческие числа: тетра (четыре), пента (пять) и так далее, вплоть до дека (десять). Последний вариант звучит как гуголдекаплекс и означает десятикратное накопительное повторение процедуры возведения числа 10 в степень его основания. Главное, не представлять себе результат. Осознать его все равно не получится, но получить травму психики – запросто.
Английская система
Однако, несмотря на простоту американской системы, в мире все же более распространена английская система, которая является системой названия чисел именно с длинной шкалой. С 1948 года ею пользуются в таких странах, как Франция, Великобритания, Испания, а также в странах – бывших колониях Англии и Испании. Построение чисел тут также довольно-таки простое: к латинскому обозначению добавляют суффикс «-иллион». Дальше же, если число в 1000 раз больше, добавляется уже суффикс «-иллиард». Как можно узнать количество спрятанных в числе нулей?
- Если число заканчивается на «-иллион», нужна будет формула 6*х + 3 («х» – это латинское числительное).
- Если число заканчивается на «-иллиард», надо будет формула 6*х + 6 (где «х», опять же, латинское числительное).
Какое число идет после гугла
Итак, мы выяснили, что чем больше число, тем реже его используют. Гугол — это 10 в 100-й степени, и им измеряют время жизни нашей Вселенной. Но какое какое значимое число идет после гугла? Оказывается, что после гугла идут еще числа, которыми люди пользуются.
8.5*10185. Это число тесно связано с другой величиной — «длина Планка». Длина Планка является очень маленькой величиной со значением 1.616199*10-35. Эта длина активно используется в квантовых вычислениях, но как она связана с нашим большим числом? Длина Планка позволяет вычислить объем Планка, который также применяется в квантовой физике. Наше число 8.5*10185 обозначает количество объемов Планка во Вселенной. Если простым языком, то наше число является попыткой посчитать объем Вселенной. Как вы понимаете, данное число является очень большим и практического применения на Земле для него не существует.
243 112 609 -1. Это число является одним из максимально массивных простых чисел, которые известны на сегодняшний день. Если его расписать, то понадобится около 13 миллионов цифр
Чем оно важно для людей? Это число несет в себе значение количества используемых объемов Планка при вычислении объемов Вселенной. То есть это не объем Вселенной, как в первом числе, а количество «измерителей ее объема».
Гуголплекс
Это число обозначает 10, возведенное в степень гугол, то есть 10, возведенное в число степени со 100 знаками. Это число является попыткой измерить количество частиц во всей Вселенной.
Число Скьюза. Это число показывает верхний предел для математических вычислений. Считается, что числа больше числа Скьюза нарушают многие математические правила и ведут себя по-другому. Даже самое меньшее число Скьюза будет намного больше гуголплекса и обозначается как: 10˄10˄10˄36, где ˄ — это возведение в степень.
Время возвращения Пуанкаре. Это достаточно сложная тема, но с довольно простым смыслом. То есть считается, что при достаточном количестве времени все становится возможным. Если просто: теорема Пуанкаре гласит, что для того, чтобы Вселенная вернулась в свое нынешнее значение, ей понадобится 10˄10˄10˄10˄10˄1.1 лет.
Бесконечность. Это число известно еще со школьной скамьи. Невозможно даже представить, как выглядят числа до это пункта и как их записывать или описывать. Бесконечность живет по своим правилам, и о ней практически ничего не известно. Правда существуют такие ученые, которые уверяют, что бесконечности не существует. А существует такое число, к которому можно прибавить 1, и получится 0.
Какое самое большое число в мире
Науке известно две разные системы исчисления – английская и американская. Следовательно, в каждой из них одно и то же число может иметь разное название. Поэтому, чтобы избежать недоразумений, необходимо разобраться в их различиях.
Американская система
Данную систему исчисления принято использовать не только в США, но и Канаде, России и ряде других стран. Научное название американской системы – числа с короткой шкалой. Название чисел в ней состоит из двух частей – порядковое число на латыни + суффикс «- иллион». Это, к примеру, триллион, октиллион и т. д. Как понять, сколько в каждом из этих чисел нулей? Для этого достаточно воспользоваться формулой 3*х+3. Х – в данном случае означает числительное на латыни.
Английская система
Конечно же, американская система исчисления достаточно простая, однако более распространенной стала английская или система с длинной шкалой. Использовать ее начали во Франции, Англии, Испании и не которых других странах в 1948 году. Аналогично американской системе, для построения числа здесь к латинскому названию добавляется суффикс «-иллион», но для чисел, которые оказываются больше в 1 тысячу раз, прибавляется уже суффикс «-иллиард». Для определения количества нулей в том или ином числе используют формулы:
- 6*х+3 – для тех чисел, которые заканчиваются на «-иллион»;
- 6*х+6 – в том случае, когда оно заканчивается на «-иллиард».
Х – в обоих случаях, это числительное на латыни.
К примеру, 10 12 в американской системе будет иметь название триллион, а в английской биллион, 1015 – квадриллион в американской и биллиард в английской системе, а 1018 – соответственно квинтиллион и триллион.
Исходя из этого, можно сделать вывод, что разные числа могут иметь одно и то же название
Поэтому, при рассмотрении определенного числа, важно предварительно узнать, какая система исчисления в данном случае используется